matlab矢量图
流线图streamline
streamline(x,y,u,v,startx,starty)其中startx,starty分别为流线的坐标
[x,y]=meshgrid(0:0.1:1,0:0.1:1);
u=sin(x);v=-y;
figure
quiver(x,y,u,v,1);
startx=0.1:0.1:1;
starty=ones(size(startx));
streamline(x,y,u,v,startx,starty)
矢量函数的可视化
%% 二维
[x,y]=meshgrid(0:.2:2);
u=cos(x).*y; v=sin(x).*y;
quiver(x,y,u,v)
%% 三维
[x,y]=meshgrid(0:.2:2);
u=cos(x).*y; v=sin(x).*y;
quiver(x,y,u,v)
梯度gradient
对于直角坐标系
∇ = ∂ ∂ x e x + ∂ ∂ y e y + ∂ ∂ z e z \nabla =\frac{\partial}{\partial x}\boldsymbol{e}_x+\frac{\partial}{\partial y}\boldsymbol{e}_y+\frac{\partial}{\partial z}\boldsymbol{e}_z
∇ = ∂ x ∂ e x + ∂ y ∂ e y + ∂ z ∂ e z
对于柱坐标系
∇ = ∂ ∂ ρ e ρ + 1 ρ ∂ ∂ φ e φ + ∂ ∂ z e z \nabla =\frac{\partial}{\partial \rho}\boldsymbol{e}_{\rho}+\frac{1}{\rho}\frac{\partial}{\partial \varphi}\boldsymbol{e}_{\varphi}+\frac{\partial}{\partial z}\boldsymbol{e}_z
∇ = ∂ ρ ∂ e ρ + ρ 1 ∂ φ ∂ e φ + ∂ z ∂ e z
对于球坐标系
∇ = ∂ ∂ r e r + 1 r ∂ ∂ θ e θ + 1 r sin θ ∂ ∂ φ e φ \nabla =\frac{\partial}{\partial r}\boldsymbol{e}_r+\frac{1}{r}\frac{\partial}{\partial \theta}\boldsymbol{e}_{\theta}+\frac{1}{r\sin \theta}\frac{\partial}{\partial \varphi}\boldsymbol{e}_{\varphi}
∇ = ∂ r ∂ e r + r 1 ∂ θ ∂ e θ + r sin θ 1 ∂ φ ∂ e φ
matlab中用法,[Fx,Fy,Fz...Fn]=gradient(F,hx,hy,hz...hn)
下面给个例子:
[x,y]=meshgrid(-2:.1:2);
z=x.*exp(-x.^2-y.^2);
[px,py]=gradient(z,.2,.2);
figure
contour(x,y,z);
hold on
quiver(x,y,px,py);
hold off
[x,y]=meshgrid(-2:.1:2);
z=x.*exp(-x.^2-y.^2);
[px,py]=gradient(z,.2,.2);
figure
contour(x,y,z);
hold on
quiver(x,y,px,py);
hold off
散度divergence
散度是单位体积的通量(即通量体密度)
d i v F = ∇ ⋅ F = lim Δ V → 0 ∬ F ⋅ d S Δ V div\boldsymbol{F}=\nabla \cdot \boldsymbol{F}=\underset{\varDelta V\rightarrow 0}{\lim}\frac{\iint{\boldsymbol{F}\cdot d\boldsymbol{S}}}{\varDelta V}
d i v F = ∇ ⋅ F = Δ V → 0 lim Δ V ∬ F ⋅ d S
直角坐标:
∇ ⋅ F = ∂ F x ∂ x + ∂ F y ∂ y + ∂ F z ∂ z \nabla \cdot \boldsymbol{F}=\frac{\partial F_x}{\partial x}+\frac{\partial F_y}{\partial y}+\frac{\partial F_z}{\partial z}
∇ ⋅ F = ∂ x ∂ F x + ∂ y ∂ F y + ∂ z ∂ F z
柱坐标:
∇ ⋅ F = 1 ρ ( ∂ ∂ ρ ( ρ F ρ ) + ∂ F φ ∂ φ + ρ ∂ F z ∂ z ) \nabla \cdot \boldsymbol{F}=\frac{1}{\rho}\left( \frac{\partial}{\partial \rho}\left( \rho F_{\rho} \right) +\frac{\partial F_{\varphi}}{\partial \varphi}+\rho \frac{\partial F_z}{\partial z} \right)
∇ ⋅ F = ρ 1 ( ∂ ρ ∂ ( ρ F ρ ) + ∂ φ ∂ F φ + ρ ∂ z ∂ F z )
球坐标:
∇ ⋅ F = 1 r 2 sin θ [ sin θ ∂ ∂ r ( r 2 F r ) + r ∂ ∂ θ ( sin θ F θ ) + r ∂ F φ ∂ φ ] \nabla \cdot \boldsymbol{F}=\frac{1}{r^2\sin \theta}\left[ \sin \theta \frac{\partial}{\partial r}\left( r^2F_r \right) +r\frac{\partial}{\partial \theta}\left( \sin \theta F_{\theta} \right) +r\frac{\partial F_{\varphi}}{\partial \varphi} \right]
∇ ⋅ F = r 2 sin θ 1 [ sin θ ∂ r ∂ ( r 2 F r ) + r ∂ θ ∂ ( sin θ F θ ) + r ∂ φ ∂ F φ ]
高斯公式:
∫ V ∇ ⋅ F d V = ∬ F ⋅ d S \int_V{\nabla \cdot \boldsymbol{F}dV}=\iint{\boldsymbol{F}\cdot d\boldsymbol{S}}
∫ V ∇ ⋅ F d V = ∬ F ⋅ d S
散度的体积分等于通量divergence
div=divergence(x,y,z,u,v,w)
syms x y z real
F=[cos(x+2*y),sin(x-2*y)];
g=divergence(F,[x y]);
divF=matlabFunction(g);
x=-2.5:0.1:2.5;
[X,Y]=meshgrid(x);
Fx=cos(X+2*Y);
Fy=sin(X-2*Y);
div_num=divF(X,Y);
pcolor(X,Y,div_num);
shading interp;
colorbar
hold on
quiver(X,Y,Fx,Fy,'k','linewidth',1);
旋度curl
矢量场旋度用来描述围绕中心旋转的程度,定义为:
r o t F = ∇ × F = lim Δ S → 0 ∮ F ⋅ d l Δ S ∣ max ⋅ n ⃗ rot\boldsymbol{F}=\nabla \times \boldsymbol{F}=\underset{\varDelta S\rightarrow 0}{\lim}\frac{\oint{\boldsymbol{F}\cdot d\boldsymbol{l}}}{\varDelta S}|_{\max}\cdot \vec{n}
r o t F = ∇ × F = Δ S → 0 lim Δ S ∮ F ⋅ d l ∣ m a x ⋅ n
对于直角坐标系:
∇ × F = ∣ e x e y e z ∂ ∂ x ∂ ∂ y ∂ ∂ z F x F y F z ∣ \nabla \times \boldsymbol{F}=\left| \begin{matrix}
\boldsymbol{e}_x& \boldsymbol{e}_y& \boldsymbol{e}_z\\
\frac{\partial}{\partial x}& \frac{\partial}{\partial y}& \frac{\partial}{\partial z}\\
F_x& F_y& F_z\\
\end{matrix} \right| ∇ × F = ∣ ∣ ∣ ∣ ∣ ∣ ∣ e x ∂ x ∂ F x e y ∂ y ∂ F y e z ∂ z ∂ F z ∣ ∣ ∣ ∣ ∣ ∣ ∣
对于柱坐标:
∇ × F = ∣ e ρ ρ e φ e z ρ ∂ ∂ ρ ∂ ∂ φ ∂ ∂ z F ρ ρ F φ F z ∣ \nabla \times \boldsymbol{F}=\left| \begin{matrix}
\frac{\boldsymbol{e}_{\rho}}{\rho}& \boldsymbol{e}_{\varphi}& \frac{\boldsymbol{e}_z}{\rho}\\
\frac{\partial}{\partial \rho}& \frac{\partial}{\partial \varphi}& \frac{\partial}{\partial z}\\
F_{\rho}& \rho F_{\varphi}& F_z\\
\end{matrix} \right| ∇ × F = ∣ ∣ ∣ ∣ ∣ ∣ ∣ ρ e ρ ∂ ρ ∂ F ρ e φ ∂ φ ∂ ρ F φ ρ e z ∂ z ∂ F z ∣ ∣ ∣ ∣ ∣ ∣ ∣
对于球坐标:
∇ × F = ∣ e r r 2 sin θ e θ r sin θ e φ r ∂ ∂ r ∂ ∂ θ ∂ ∂ φ F r r F θ r sin θ F φ ∣ \nabla \times \boldsymbol{F}=\left| \begin{matrix}
\frac{\boldsymbol{e}_r}{r^2\sin \theta}& \frac{\boldsymbol{e}_{\theta}}{r\sin \theta}& \frac{\boldsymbol{e}_{\varphi}}{r}\\
\frac{\partial}{\partial r}& \frac{\partial}{\partial \theta}& \frac{\partial}{\partial \varphi}\\
F_r& rF_{\theta}& r\sin \theta F_{\varphi}\\
\end{matrix} \right| ∇ × F = ∣ ∣ ∣ ∣ ∣ ∣ ∣ r 2 s i n θ e r ∂ r ∂ F r r s i n θ e θ ∂ θ ∂ r F θ r e φ ∂ φ ∂ r sin θ F φ ∣ ∣ ∣ ∣ ∣ ∣ ∣
matlab中用curl函数
syms x y z real
F=[cos(x+2*y),sin(x-2*y)];
G=curl([F,0],[x y z])
curlF=matlabFunction(G(3));
x=-2.5:0.1:2.5;
[X,Y]=meshgrid(x);
Fx=cos(X+2*Y);
Fy=sin(X-2*Y);
rot=curlF(X,Y);
pcolor(X,Y,rot);
shading interp;
colorbar
hold on
quiver(X,Y,Fx,Fy,'k','linewidth',1);
拉普拉斯算子
定义:
Δ = ∇ ⋅ ∇ = ∇ 2 = ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 + ∂ 2 ∂ z 2 \Delta =\nabla \cdot \nabla =\nabla ^2=\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}+\frac{\partial ^2}{\partial z^2}
Δ = ∇ ⋅ ∇ = ∇ 2 = ∂ x 2 ∂ 2 + ∂ y 2 ∂ 2 + ∂ z 2 ∂ 2
矢量函数拉普拉斯变换:
Δ F = ∇ ( ∇ ⋅ F ) − ∇ × ( ∇ × F ) \Delta \boldsymbol{F}=\nabla \left( \nabla \cdot \boldsymbol{F} \right) -\nabla \times \left( \nabla \times \boldsymbol{F} \right)
Δ F = ∇ ( ∇ ⋅ F ) − ∇ × ( ∇ × F )
syms x y z
V=[x^2*y,y^2*z,z^2*x];
vars=[x y z];
gradient(divergence(V,vars))-curl(curl(V,vars),vars)
数值差分法del2(U,hx,hy,hz...hn)
L i , j = 1 4 ( U i , j + 1 + U i + 1 , j + U i − 1 , j + U i , j − 1 ) − U i , j L_{i,j}=\frac{1}{4}\left( U_{i,j+1}+U_{i+1,j}+U_{i-1,j}+U_{i,j-1} \right) -U_{i,j}
L i , j = 4 1 ( U i , j + 1 + U i + 1 , j + U i − 1 , j + U i , j − 1 ) − U i , j
故del2求出的是拉普拉斯运算的1/4
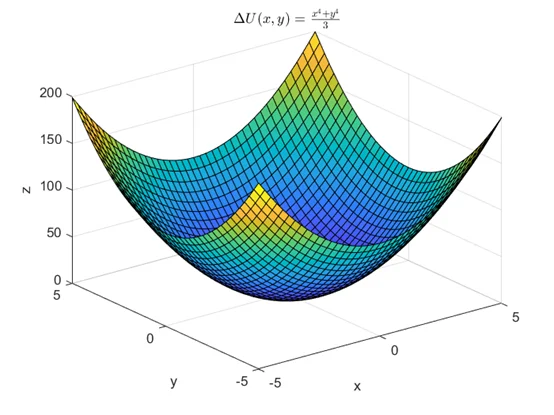
[x,y]=meshgrid(-5:0.25:5);
U=1/3.*(x.^4+y.^4);
h=0.25;%指定步长
L=4*del2(U,h);
figure
surf(x,y,L);
grid on
title('$\Delta U(x,y)=\frac{x^4+y^4}{3}$','Interpreter','latex');
xlabel('x')
ylabel('y')
zlabel('z')