随机过程

随机过程的数字特征

平稳随机过程

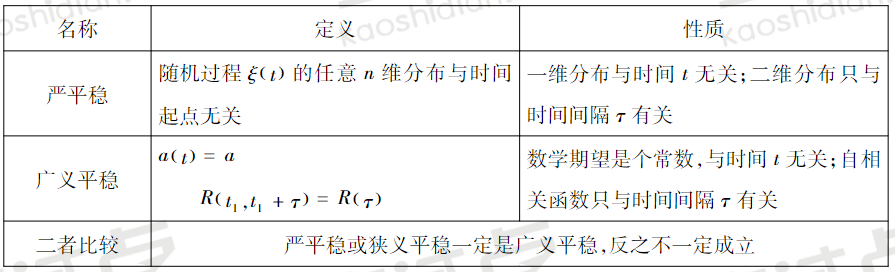
严平稳和广义平稳随机过程

各态历经性

任取平稳随机过程$\xi(t)$的任一样本函数$x(t)$，其时间均值和时间自相关满足:

\begin{equation} \begin{gathered} \bar{a}=\overline{x(t)}=\lim _{T \rightarrow \infty} \frac{1}{T} \int_{-T / 2}^{T / 2} x(t) d t=a \\ \overline{R(\tau)}=\overline{x(t) x(t+\tau)}=\lim _{T \rightarrow \infty} \frac{1}{T} \int_{-T / 2}^{T / 2} x(t) x(t+\tau) d t=R(\tau) \end{gathered} \end{equation}

意义：可用任意一次实现的“样本平均”来取代随机过程的“统计平均”，可用任意一次实现的功率谱密度来取代随机过程的功率谱密度，简化测量和计算问题；具有各态历经性的随机过程一定是平稳随机过程，反之不一定成立

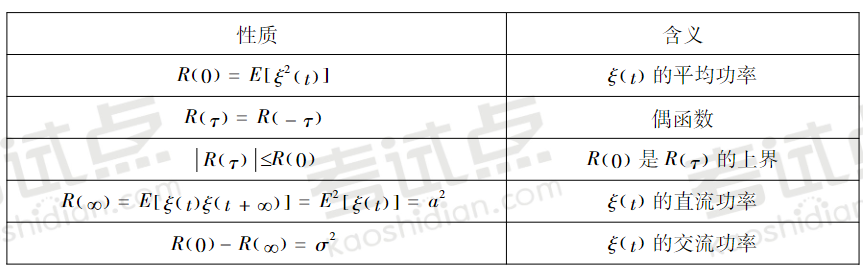
平稳随机过程自相关函数的性质

维纳———辛钦定理

平稳随机过程的自相关函数和功率谱密度互为傅里叶变换对。

高斯随机过程

定义：任意ｎ维概率密度都服从正态分布的随机过程。

重要性质：高斯过程若广义平稳，则必狭义平稳；高斯过程中的随机变量之间若不相关，则它们统计独立；若干个高斯过程之和仍是高斯过程；高斯过程经线性变换后，仍是高斯过程.

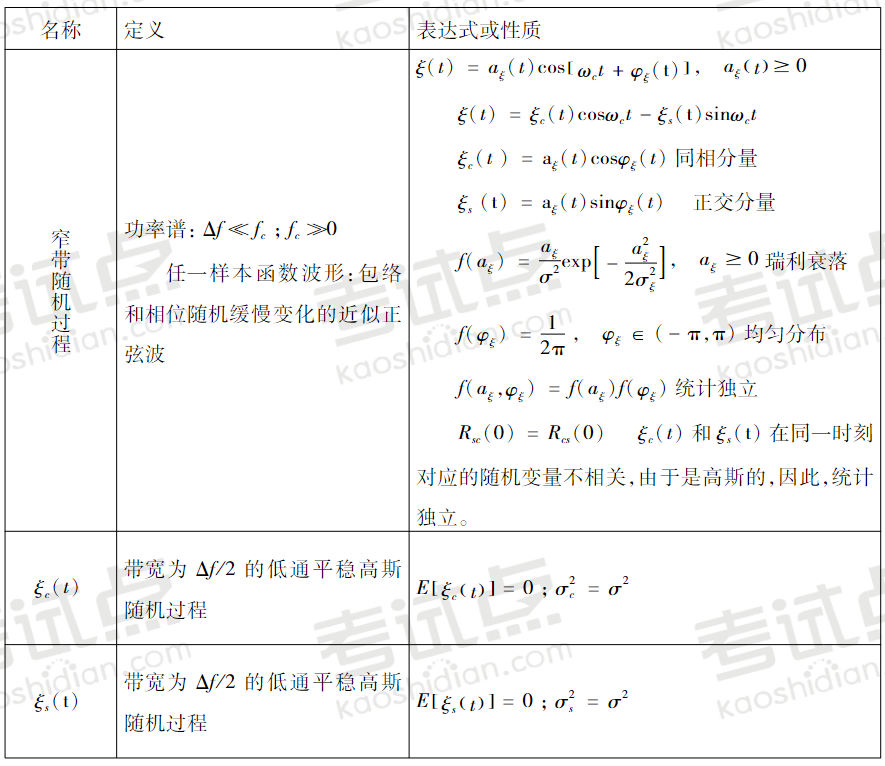
均值为０，方差为σ２的平稳高斯窄带随机过程的定义及性质:

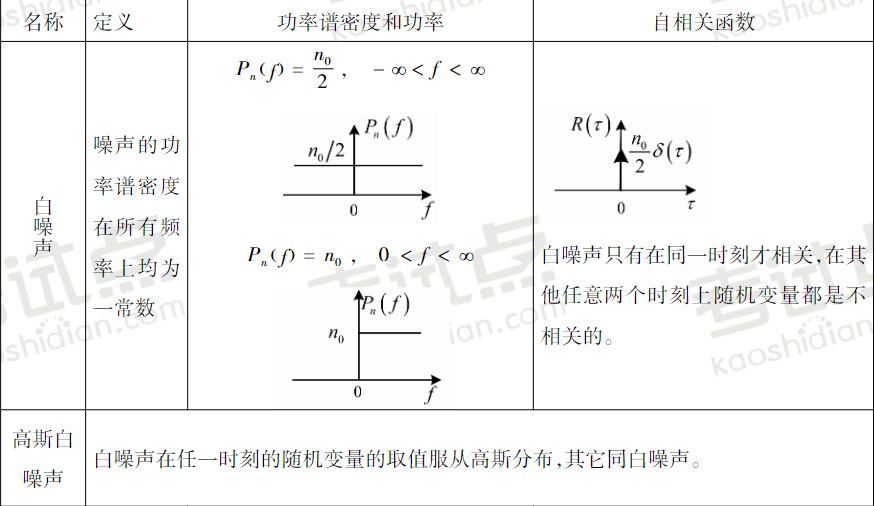
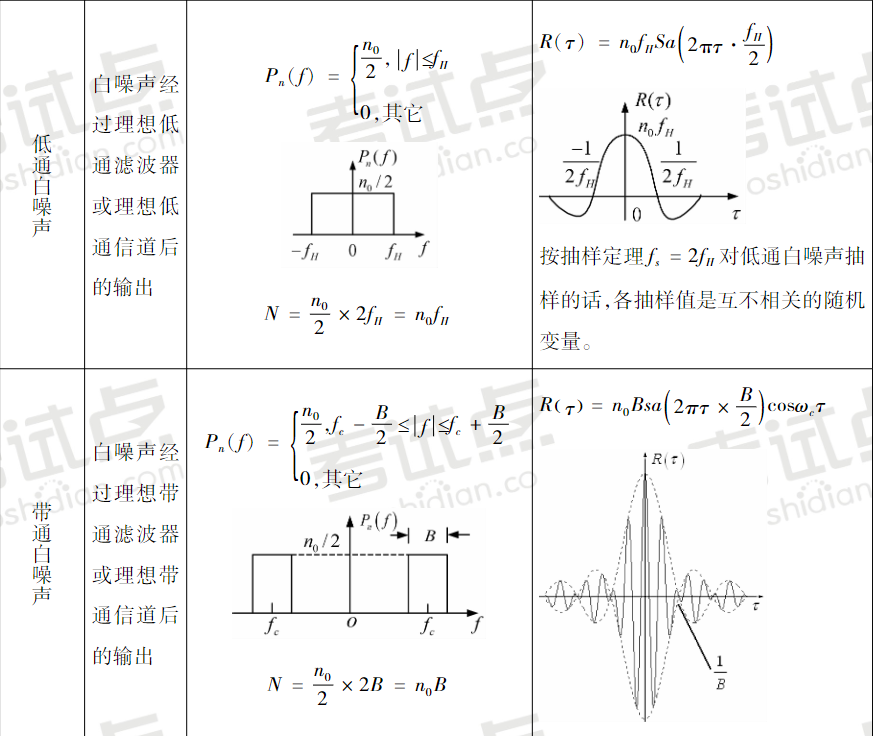
高斯白噪声和带限白噪声