差错控制编码

差错控制编码属于信道编码：

• 目的：克服信道噪声及其他干扰引起的误码，提高传输的可靠性。
• 基本原理：信道编码器在信息码元序列中按照一定的关系加入一些冗余码元(也即监督码元)，信道译码器利用这种关系发现或纠正可能存在的错码。

差错控制方式：

• 检错重发(ARQ)
• 前向纠错(FEC)
• 检错删除
• 反馈校验

编码类型：

• 线性码：监督吗和信息码关系由一组线性方程确定。可分为分组码和非分组码。
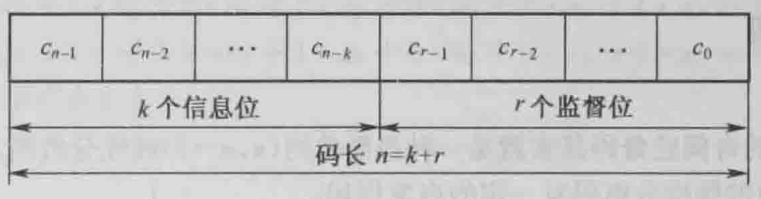
• 分组码：结构如下图所示。它是把信息序列以k个码元分为-组,通过编码器把每个信息组(k个信息码元)按定规则产生r个监督(校验)码元，从而构成每组长度为n=k+r的具有纠检功能的编码集合。因此，分组码中的每一码组的监督元仅与本组中的信息元有关。
  
• 卷积码:监督码元不仅和当前的一段信 息码元有关，而且还同前 面若干个信息段码元也有约束关系。卷积码是非分组码的一一种。

码长、码重、码距的概念

最小码距$d_0$与纠检错能力：$d_0$决定了编码的纠检错能力，对于分组码来说：

• 检测$e$个错码，要求：

$d_0 \ge e+1$

• 纠正$t$个错码，要求：

$d_0 \ge 2t+1$

• 纠$t$个同时可检$e$个错码。要求：

$d_0 \ge e+t+1 \text{且}e>t$

• 编码效率：$R_c = k/n$
• 编码增益：在保持误码率恒定条件下，采用纠错编码所节省的信噪比称为编码增益。

线性分组码

下面以举例为主：

监督方程：

$\left\{\begin{array}{l} 1 \cdot a_{6}+1 \cdot a_{5}+1 \cdot a_{4}+0 \cdot a_{3}+1 \cdot a_{2}+0 \cdot a_{1}+0 \cdot a_{0}=0 \\ 1 \cdot a_{6}+1 \cdot a_{5}+0 \cdot a_{4}+1 \cdot a_{3}+0 \cdot a_{2}+1 \cdot a_{1}+0 \cdot a_{0}=0 \\ 1 \cdot a_{6}+0 \cdot a_{5}+1 \cdot a_{4}+1 \cdot a_{3}+0 \cdot a_{2}+0 \cdot a_{1}+1 \cdot a_{0}=0 \end{array}\right.$

矩阵形式：

$\left[\begin{array}{l} 1110100 \\ 1101010 \\ 1011001 \end{array}\right]\left[\begin{array}{l} a_{6} \\ a_{5} \\ a_{4} \\ a_{3} \\ a_{2} \\ a_{1} \\ a_{0} \end{array}\right]=\left[\begin{array}{l} 0 \\ 0 \\ 0 \end{array}\right]$

记作：

$\mathbf{H}\cdot \mathbf{A}^T = \mathbf{0}^T$

$\mathbf{H}$称为监督矩阵，形状为$(r, n)$且可以初等变换化简为典型监督矩阵：

$\boldsymbol{H}=\left[ \boldsymbol{P}_{r\times k}\,\,\boldsymbol{I}_r \right]$

生成监督位方程：

$\left[\begin{array}{l} d_{2} \\ a_{1} \\ a_{0} \end{array}\right]=\left[\begin{array}{l} 1110 \\ 1101 \\ 1011 \end{array}\right]\left[\begin{array}{l} a_{6} \\ a_{5} \\ a_{4} \\ a_{3} \end{array}\right]$

$\boldsymbol{G}=\left[ \boldsymbol{I}_k\,\,\boldsymbol{Q}_{k\times r} \right]$

通过生成矩阵，我们将信息位码字转化为整个码字：

$\boldsymbol{A}=\left[ a_6\,\,a_5\,\,a_4\,\,a_3 \right] \cdot \boldsymbol{G}$

并且$\boldsymbol{Q}_{k\times r}$和$\boldsymbol{P}_{r\times k}$互为转置。

汉明码

对线性分组码当$n=2^r-1$时就是汉明码。
汉明码是能纠1位错码的高效线性分组码。

校正子和译码

设接收码元组为$\boldsymbol{B}$，定义校正子$\boldsymbol{S}$：

$\boldsymbol{B}\cdot \boldsymbol{H}^T=\boldsymbol{S}$

若$\boldsymbol{S}=0$则无错或检测不出错误。
设错误图样为$\boldsymbol{E}$，则

$\boldsymbol{A}=\boldsymbol{B}-\boldsymbol{E}=\boldsymbol{B}+\boldsymbol{E}$

因此易知：

$\boldsymbol{S}=\boldsymbol{E}\cdot \boldsymbol{H}^T$

根据上述三个式子便可根据接收码组$\boldsymbol{B}$和监督矩阵$\boldsymbol{H}$中纠错得到发送码组$\boldsymbol{A}$

线性分组码性质：

• 具有封闭性，即任意两个许用码组之和(逐位模2加)仍为一需用码组
• 它的最小码距$d_0$等于非全零码组的最小重量

循环码

循环码属于线性分组码，循环码还具有循环性，循环码中任一码组经过循环移位后仍为一个许用码组。

码多项式$A(x)$

例如码组(1100101)可表示为：

$A(x)=x^6+x^5+x^2+1$

生成多项式$g(x)$

存在性：

• $(n,k)$循环码中，有且仅有一个次数为$(n-k)$的多项式：
  $g(x)=1 \cdot x^{n-k}+a_{n-k-1} x^{n-k-1}+\cdots+a_{1} x+1$
  $g(x)$为生成多项式，$g(x)$决定了循环码的纠错能力。

性质：

• $g(x)$是$x^n+1$的一个因式
• 所有码多项式$A(x)$都可以被$g(x)$整除，而且任意一个次数不大于$(k-1)$的多项式乘$g(x)$都是码多项式

生成矩阵$G$

$\boldsymbol{G}(x)=\left[\begin{array}{c} x^{k-1} g(x) \\ x^{k}-2^{2} g(x) \\ \vdots \\ x g(x) \\ g(x) \end{array}\right]$

循环码的编码

$A(x)=x^{n-k} m(x)+r(x)$

$r(x)$作为余式，代表监督码元。$m(x)$为信息码多项式，$x^{n-k}$目的是预留给监督位位置。以$g(x)=x^4+x^2+x+1$为例：

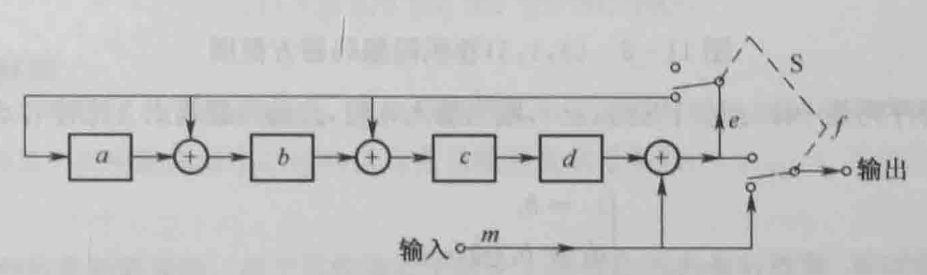
循环码的译码

• 检错：
  对接收码组$B(x)$进行：

$B(x)/g(x)$

若能除尽，则表示无错，若除不尽则发生错误

• 纠错：
  • 用接收码组$B(x)$除以生成多项式$g(x)$得到余式，也就是校正子多项式$S(x)$
  • 由$S(x)$查表或通过计算得到错误图样$E(x)$，确定错码位置
  • $A(x)=B(x)-E(x)$

卷积码(非分组码)

分组码是把$k$个信息比特的序列编成$n$个比特的码组，每个码组的$n-k$个校验位与本码组的$k$个信息位有关，而与其他码组无关。为了达到一定的纠错能力和编码效率，分组码的长度一般都比较大。编译码时必须把整个信息码组存储起来，由此产生的译码延时随n的增加而增加。

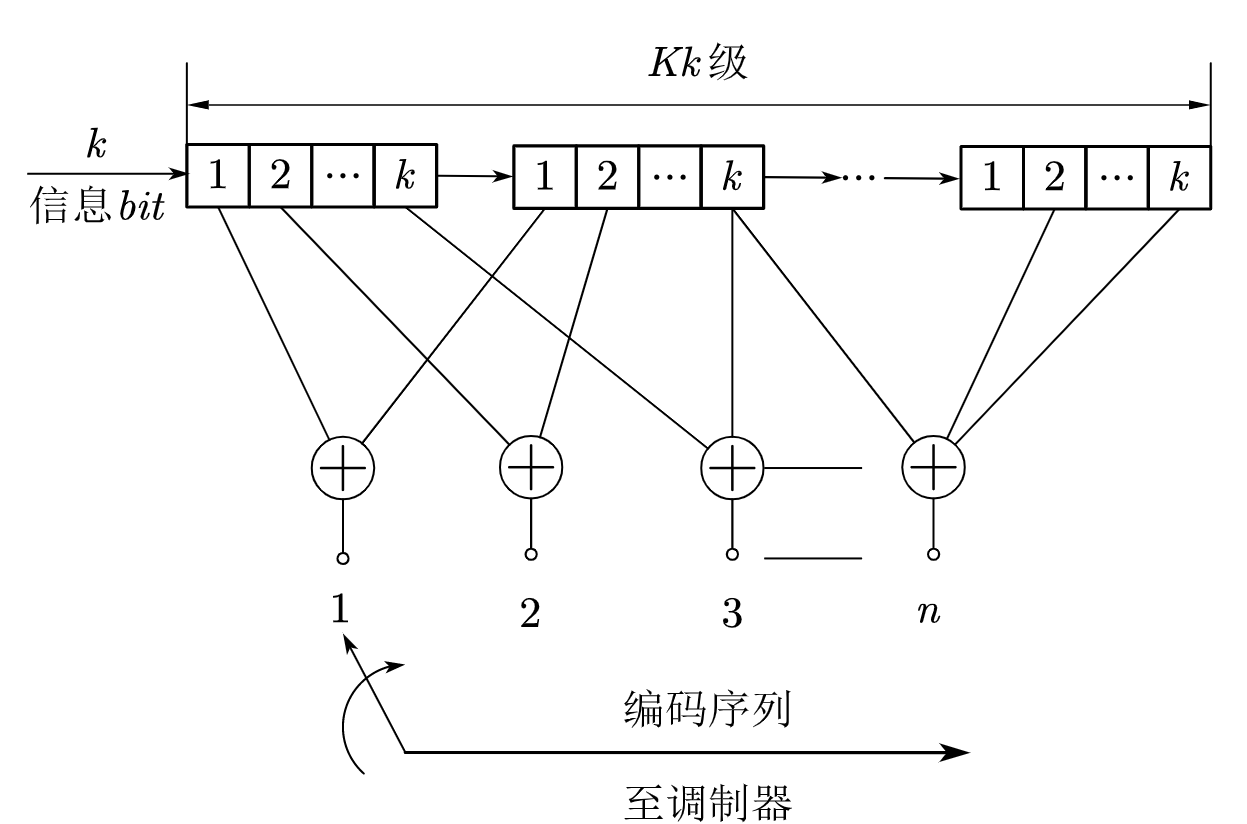
卷积码是一个有限记忆系统，如上图所示，它也将信息序列分割成长度$k$的一个个分组，然后将$k$个信息比特编成$n$个比特，但$k$和$n$通常很小，特别适合以串行形式进行传输，时延小。与分组码不同的是在某一分组编码时，不仅参看本时刻的分组而且参看以前的$N-1$个分组，编码过程中互相关联的码元个数为$nN$。$N$称为约束长度。常把卷积码写成$(n，k，N-1)$卷积码。正因为卷积码在编码过程中，充分利用了各级之间的相关性，无论是从理论上还是实际上均已证明其性能要优于分组码。卷积编码过程如下图：

卷积码的译码方式常采用基于似然法的维特比译码法：

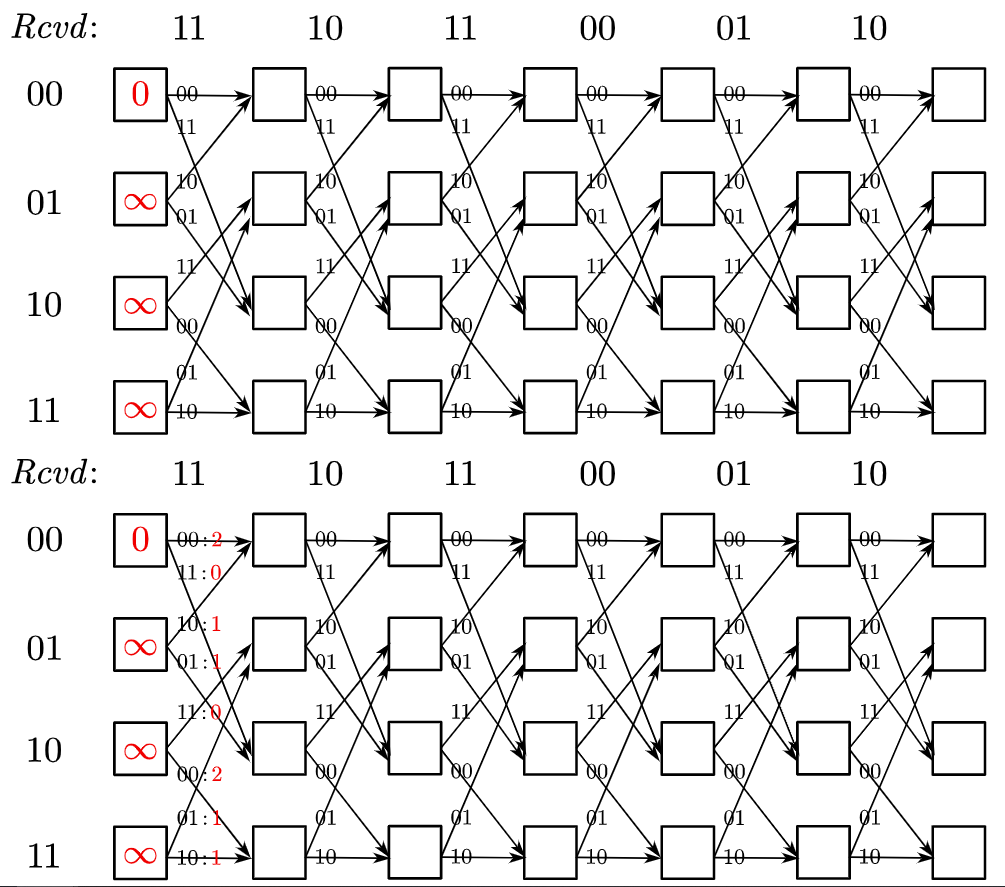
常采用软判决和硬判决，详情请看我的课设论文：