数学期望

概率论

之前被问一个概率论的题目，这里分享一下我的解法：

问题

问题一：

$\left( 1 \right) x_1+x_2+x_3+x_4\le 1, 0\le x_i\le 1$

求：$\mathbb{E} \left( x_1x_2x_3x_4 \right) $

问题二：

$\left( 2 \right) x_1+x_2+x_3+x_4\le 1\text{，}0\le x_i\le 1$

且$x_1+x_2=\frac{1}{2},x_3+x_4=\frac{1}{2}$
求：$\mathbb{E} \left( x_1x_2x_3x_4 \right) $

误区

首先一个误区是就是考虑$x_i$是均匀分布，我们先假设$x_i$为均匀分布，则有：

\begin{equation} \begin{split} \mathbb{E}& \left( x_1+x_2+x_3+x_4 \right) =4\mathbb{E} \left( x_1 \right)\\ &=4\int_0^1{x_1dx_1}=2 \end{split} \nonumber \end{equation}

我们又知道：

$\mathbb{E} \left( x_1+x_2+x_3+x_4 \right) \le \mathbb{E} \left( 1 \right) =1$

因此产生矛盾，即$x_i$是均匀分布不成立。如下正解

问题一解答

设$x_1+x_2+x_3+x_4$是均匀分布的，那么：

\begin{equation} \iiiint_{ x_1+ x_2 + x_3 + x_4 \le 1}{dx_1 dx_2 dx_3 dx_4} =1 \end{equation}

\begin{equation} \begin{split} \frac{\partial^2 f}{\partial{x^2}} &= \frac{\partial(\Delta_x f(i,j))}{\partial x} = \frac{\partial(f(i+1,j)-f(i,j))}{\partial x} \\ &= \frac{\partial f(i+1,j)}{\partial x} - \frac{\partial f(i,j)}{\partial x} \\ &= f(i+2,j) -2f(f+1,j) + f(i,j) \end{split} \nonumber \end{equation}

则有：

\begin{equation} \begin{split} f\left( x_1,x_2,x_3,x_4 \right) &=\frac{1}{\iiiint_{x_1+x_2+x_3+x_4\le 1}{dx_1dx_2dx_3dx_4}}\\ &=\frac{1}{\int_0^1{dx_1}\int_0^{1-x_1}{dx_2}\int_0^{1-x_1-x_2}{dx_3}\int_0^{1-x_1-x_2-x_3}{dx_4}}\\ &=\frac{1}{\int_0^1{dx_1}\int_0^{1-x_1}{dx_2}\int_0^{1-x_1-x_2}{\left( 1-x_1-x_2-x_3 \right) dx_3}}\\ &=\frac{1}{\int_0^1{dx_1}\int_0^{1-x_1}{\frac{\left( 1-x_1-x_2 \right) ^2}{2}dx_2}}\\ &=\frac{1}{\int_0^1{dx_1}\int_0^{1-x_1}{\frac{x_{2}^{2}}{2}dx_2}}\\ &=\frac{1}{\int_0^1{\frac{\left( 1-x_1 \right)^3}{6}dx_1}}\\ &=\frac{1}{\int_0^1{\frac{x_1^3}{6}dx_1}}\\ &=24 \end{split} \nonumber \end{equation}

因此得到其概率密度为：

$f\left( x_1,x_2,x_3,x_4 \right) =\begin{cases} 24 \quad 0\le x_1+x_2+x_3+x_4\le 1\text{，}0\le x_i\le 1\text{，}\\ 0 \quad \quad \quad \quad \quad \mathrm{else}\\ \end{cases}$

因此我们可以求出期望：

\begin{equation} \begin{split} \mathbb{E} \left( x_1x_2x_3x_4 \right) &=\iiiint_{\varOmega}{24x_1x_2x_3x_4dx_1dx_2dx_3dx_4}\\ &=24\int_0^1{x_1dx_1}\int_0^{1-x_1}{x_2dx_2}\int_0^{1-x_1-x_2}{x_3dx_3}\int_0^{1-x_1-x_2-x_3}{x_4dx_4}\\ &=24\int_0^1{x_1dx_1}\int_0^{1-x_1}{x_2dx_2}\int_0^{1-x_1-x_2}{x_3\frac{\left( 1-x_1-x_2-x_3 \right) ^2}{2}dx_3}\\ &=24\int_0^1{x_1dx_1}\int_0^{1-x_1}{x_2dx_2}\int_0^{1-x_1-x_2}{x_3\frac{\left( 1-x_1-x_2-x_3 \right) \left( 1-x_1-x_2 \right)}{4}dx_3}\\ &=24\int_0^1{x_1dx_1}\int_0^{1-x_1}{x_2\left[ \frac{\left( 1-x_1-x_2 \right) ^4}{24} \right] dx_2}\\ &=\int_0^1{x_1\frac{\left( 1-x_1 \right) ^6}{30}dx_1}\\ &=\frac{1}{56\times 30}=0.000595238 \end{split} \nonumber \end{equation}

问题二解答

问题二也即：

$0\le x_i\le \frac{1}{2}\text{，且}x_1+x_2=\frac{1}{2},x_3+x_4=\frac{1}{2}$

$\text{求}\mathbb{E} \left( x_1x_2x_3x_4 \right)$

也即：

$0\le x_i\le \frac{1}{2}\text{，且}x_1+x_2=\frac{1}{2}$

求$\left[ \mathbb{E} \left( x_1x_2 \right) \right] ^2$
由于

\begin{equation} \begin{split} \mathbb{E} \left( x_1x_2 \right) &=\mathbb{E} \left( x_1\left( \frac{1}{2}-x_1 \right) \right)\\ &=\frac{1}{2}\mathbb{E} \left( x_1 \right) -\mathbb{E} \left( x_{1}^{2} \right) \\ &=\frac{1}{2}\times \frac{1}{4}-\int_0^{\frac{1}{2}}{2x^2dx}\\ &=\frac{1}{24} \end{split} \nonumber \end{equation}

因此：

$\left[ \mathbb{E} \left( x_1x_2 \right) \right] ^2=\left( \frac{1}{24} \right) ^2=0.00173611$

计算机验证

clear;close all;
num = 100000;s1=0;N=0;
for i=1:num
    x1 = rand;x2 = rand; x3 = rand; x4 = rand;
    if x1+x2+x3+x4 <= 1
        z1=x1*x2*x3*x4;N=N+1;
        scatter(N,z1,8,'r')
        hold on;
        s1=s1+z1;
    end
end
s1_mean=s1/N
clear s2;
s2=0;
for i=1:N
    x1 = 1/2*rand;  x3 = 1/2*rand;
    z2=x1*(1/2-x1)*x3*(1/2-x3);
    scatter(i,z2,8,'g')
    s2=s2+z2;
end
s2_mean=s2/N

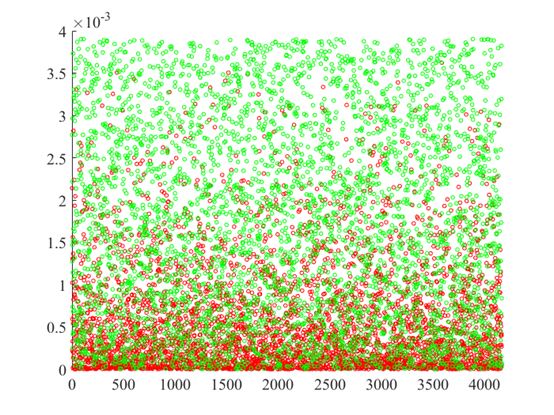
数值模拟的平均为：

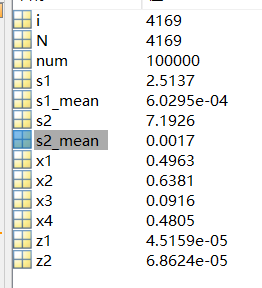
验证成功。