SVD奇异分解

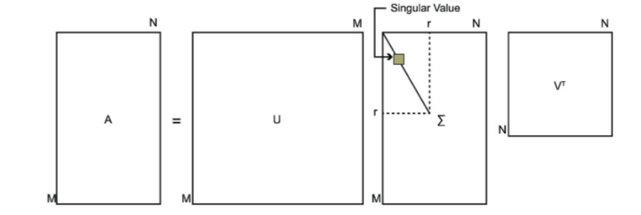
SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m×n的矩阵，那么我们定义矩阵A的SVD为：

$A=U\varSigma V^T$

其中$U$是一个$m\times m$的矩阵，$\varSigma$是一个$m\times n$除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值，$V$是一个$n\times n$的矩阵。$U$和$V$都是酉矩阵，即满足

$U^TU=I, \quad V^T V =I$

SVD分解步骤：

• step1:求$V$

求$A^TA$(大小为$n\times n$)的特征值和特征向量：

$(A^TA)v_i=\lambda_i v_i$

所有特征向量组成矩阵$V$
，$V$中的每个特征向量叫做$A$的右奇异向量。

• step2:求$U$

求$AA^T$(大小为$m\times m$)的特征值和特征向量：

$(AA^T)u_i=\lambda_i u_i$

所有特征向量组成矩阵$U$
，$U$中的每个特征向量叫做$A$的左奇异向量。

• step3：求$\varSigma$

$A=U \Sigma V^{T} \Rightarrow A V=U \Sigma V^{T} V \Rightarrow A V=U \Sigma \Rightarrow A v_{i}=\sigma_{i} u_{i} \Rightarrow \sigma_{i}=A v_{i} / u_{i}$

进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方，也就是说特征值和奇异值满足如下关系：

$A=U \Sigma V^{T} \Rightarrow A^{T}=V \Sigma U^{T} \Rightarrow A^{T} A=V \Sigma U^{T} U \Sigma V^{T}=V \Sigma^{2} V^{T}$

由此可以看出

$\sigma_{i}=\sqrt{\lambda_{i}}$

可从此计算奇异值

举例

$\mathbf{A}=\left(\begin{array}{ll} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}\right)$

首先求出$A^TA$和$AA^T$：

$\begin{gathered} \mathbf{A}^{\mathbf{T}} \mathbf{A}=\left(\begin{array}{lll} 0 & 1 & 1 \\ 1 & 1 & 0 \end{array}\right)\left(\begin{array}{ll} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}\right)=\left(\begin{array}{ll} 2 & 1 \\ 1 & 2 \end{array}\right) \\ \mathbf{A} \mathbf{A}^{\mathbf{T}}=\left(\begin{array}{ll} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}\right)\left(\begin{array}{lll} 0 & 1 & 1 \\ 1 & 1 & 0 \end{array}\right)=\left(\begin{array}{lll} 1 & 1 & 0 \\ 1 & 2 & 1 \\ 0 & 1 & 1 \end{array}\right) \end{gathered}$

进而求出$A^TA$的特征值和特征向量：

$\lambda_{1}=3 ; v_{1}=\left(\begin{array}{c} 1 / \sqrt{2} \\ 1 / \sqrt{2} \end{array}\right) ; \lambda_{2}=1 ; v_{2}=\left(\begin{array}{c} -1 / \sqrt{2} \\ 1 / \sqrt{2} \end{array}\right)$

接着求出$AA^T$的特征值和特征向量：

$\lambda_{1}=3 ; u_{1}=\left(\begin{array}{c} 1 / \sqrt{6} \\ 2 / \sqrt{6} \\ 1 / \sqrt{6} \end{array}\right) ; \lambda_{2}=1 ; u_{2}=\left(\begin{array}{c} 1 / \sqrt{2} \\ 0 \\ -1 / \sqrt{2} \end{array}\right) ; \lambda_{3}=0 ; u_{3}=\left(\begin{array}{c} 1 / \sqrt{3} \\ -1 / \sqrt{3} \\ 1 / \sqrt{3} \end{array}\right)$

利用$Av_i=\sigma_i u_i , i=1,2$求奇异值：

$\begin{aligned} &\left(\begin{array}{ll} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}\right)\left(\begin{array}{c} 1 / \sqrt{2} \\ 1 / \sqrt{2} \end{array}\right)=\sigma_{1}\left(\begin{array}{c} 1 / \sqrt{6} \\ 2 / \sqrt{6} \\ 1 / \sqrt{6} \end{array}\right) \Rightarrow \sigma_{1}=\sqrt{3} \\ &\left(\begin{array}{ll} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}\right)\left(\begin{array}{c} -1 / \sqrt{2} \\ 1 / \sqrt{2} \end{array}\right)=\sigma_{2}\left(\begin{array}{c} 1 / \sqrt{2} \\ 0 \\ -1 / \sqrt{2} \end{array}\right) \Rightarrow \sigma_{2}=1 \end{aligned}$

也可以用$\sigma_i=\sqrt{\lambda_i}$直接求出奇异值为$\sqrt{3}$和1，最终得到A的奇异值分解为：

$A=U \Sigma V^{T}=\left(\begin{array}{ccc} 1 / \sqrt{6} & 1 / \sqrt{2} & 1 / \sqrt{3} \\ 2 / \sqrt{6} & 0 & -1 / \sqrt{3} \\ 1 / \sqrt{6} & -1 / \sqrt{2} & 1 / \sqrt{3} \end{array}\right)\left(\begin{array}{cc} \sqrt{3} & 0 \\ 0 & 1 \\ 0 & 0 \end{array}\right)\left(\begin{array}{cc} 1 / \sqrt{2} & 1 / \sqrt{2} \\ -1 / \sqrt{2} & 1 / \sqrt{2} \end{array}\right)$

python和matlab都有内置的函数。