位姿的数学描述

旋转矩阵

相机可以看成三维空间的刚体，于是位置是指相机在空间中的哪个地方，而姿态则是指相机的朝向。

内积可以描述向量间的投影关系。
外积表示向量的旋转。

$\boldsymbol{a} \times \boldsymbol{b}=\left[\begin{array}{ccc} i & j & k \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \end{array}\right]=\left[\begin{array}{c} a_{2} b_{3}-a_{3} b_{2} \\ a_{3} b_{1}-a_{1} b_{3} \\ a_{1} b_{2}-a_{2} b_{1} \end{array}\right]=\left[\begin{array}{ccc} 0 & -a_{3} & a_{2} \\ a_{3} & 0 & -a_{1} \\ -a_{2} & a_{1} & 0 \end{array}\right] \boldsymbol{b} \triangleq \boldsymbol{a}^{\wedge} \boldsymbol{b}$

$\boldsymbol{a}^{\wedge}$记为$\boldsymbol{a}$反对称矩阵。

我们设某个单位正交基 $(e_1, e_2, e_3)$ 经过一次旋转， 变成了$( e _ { 1 } ^ { \prime } , e _ { 2 } ^ { \prime } , e _ { 3 } ^ { \prime } )$。我们有：

$\left[e_{1}, e_{2}, e_{3}\right]\left[\begin{array}{c} a_{1} \\ a_{2} \\ a_{3} \end{array}\right]=\left[e_{1}^{\prime}, e_{2}^{\prime}, e_{3}^{\prime}\right]\left[\begin{array}{c} a_{1}^{\prime} \\ a_{2}^{\prime} \\ a_{3}^{\prime} \end{array}\right]$

可以写为：

$\left[\begin{array}{c} a_{1} \\ a_{2} \\ a_{3} \end{array}\right]=\left[\begin{array}{lll} e_{1}^{T} e_{1}^{\prime} & e_{1}^{T} e_{2}^{\prime} & e_{1}^{T} e_{3}^{\prime} \\ e_{2}^{T} e_{1}^{\prime} & e_{2}^{T} e_{2}^{\prime} & e_{2}^{T} e_{3}^{\prime} \\ e_{3}^{T} e_{1}^{\prime} & e_{3}^{T} e_{2}^{\prime} & e_{3}^{T} e_{3}^{\prime} \end{array}\right]\left[\begin{array}{c} a_{1}^{\prime} \\ a_{2}^{\prime} \\ a_{3}^{\prime} \end{array}\right] \triangleq R a^{\prime} .$

这个矩阵由两组基之间的内积组成，刻 画了旋转前后同一个向量的坐标变换关系。

旋转矩阵的集合定义为：

$S O ( n ) = \{ R \in \mathbb{R} ^ { n \times n } | R R ^ { T } = I , det( R ) = 1 \}$

变换矩阵

$\left[\begin{array}{l} a^{\prime} \\ 1 \end{array}\right]=\left[\begin{array}{cc} R & t \\ 0^{T} & 1 \end{array}\right]\left[\begin{array}{l} a \\ 1 \end{array}\right] \triangleq T\left[\begin{array}{l} a \\ 1 \end{array}\right]$

矩阵$ T $称为变换矩阵。

矩阵又称为特殊欧氏群（Special Euclidean Group）：

$S E(3)=\left\{T=\left[\begin{array}{cc} R & t \\ 0^{T} & 1 \end{array}\right] \in \mathbb{R}^{4 \times 4} \mid R \in S O(3), t \in \mathbb{R}^{3}\right\}$

求解该矩阵的逆表示一个反向的变换：

$T^{-1}=\left[\begin{array}{cc} R^{T} & -R^{T} t \\ 0^{T} & 1 \end{array}\right]$

旋转向量

任意旋转都可以用一个旋转轴和一个旋转角。这种表示法只需一个三维向量即可描述旋转。同样，对于变换矩阵，我们使用一个旋转向量和一个平移向量即可表达一次变换。这时的维数正好是六维。

设旋转轴为$\boldsymbol{n}$，旋转角为$\theta$，它对应的旋转向量为$\theta \boldsymbol{n}$。

旋转向量到旋转矩阵的过程由罗德里格斯公式（Rodrigues’s Formula ）表明：

$\boldsymbol{R} = \cos \theta \boldsymbol{I} + ( 1 - \cos \theta ) \boldsymbol{n} ^ { T } + \sin \theta \boldsymbol{n} ^ { \wedge }$

$\theta = \arccos ( \frac { tr ( R ) - 1 } { 2 } )$

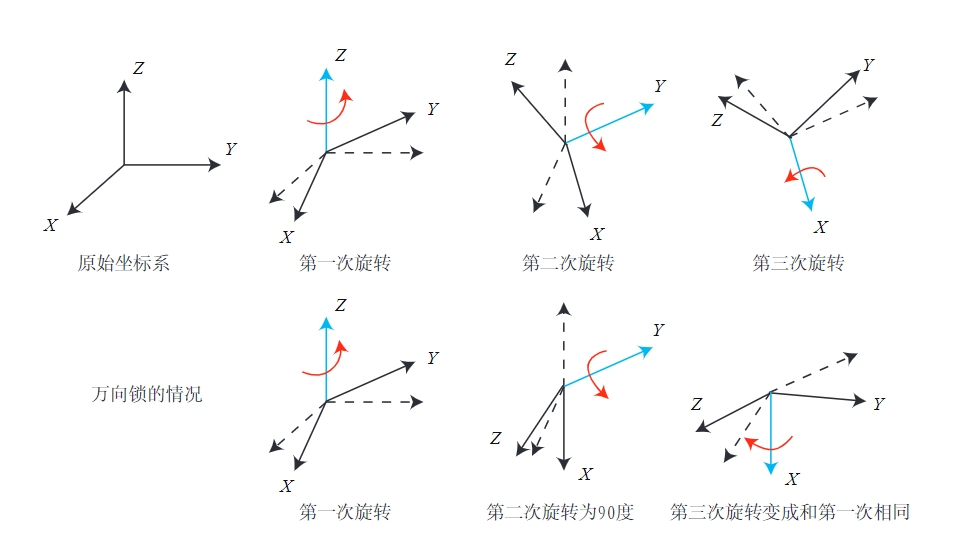
欧拉角

欧拉角则提供了一种非常直观的方式来 描述旋转——它使用了三个分离的转角，把一个旋转分解成三次绕不同轴的旋转：

1. 绕物体的 Z 轴旋转，得到偏航角 yaw；
2. 绕旋转之后的 Y 轴旋转，得到俯仰角 pitch；
3. 绕旋转之后的 X 轴旋转，得到滚转角 roll。

欧拉角的一个重大缺点是会碰到著名的万向锁问题，欧拉角不适于插值和迭代，往往只用于人机交互中。

四元数

找不到不带奇异性的三维向量描述方式，。三维旋转是一个三维流形，想要无奇异性地表达它，用三个量是不够的。

四元数 是 Hamilton 找到的一种扩展的复数. 它既是紧凑的，也没有奇异性。

$\boldsymbol{q} = q _ { 0 } + q _ { 1 } i + q _ { 2 } j + q _ { 3 } k _ { y }$

$\left\{\begin{array}{l} i^{2}=j^{2}=k^{2}=-1 \\ i j=k, j i=-k \\ j k=i, k j=-i \\ k i=j, i k=-j \end{array}\right.$

$\boldsymbol{q}=[s, \boldsymbol{v}], \quad s=q_{0} \in \mathbb{R}, \boldsymbol{v}=\left[q_{1}, q_{2}, q_{3}\right]^{T} \in \mathbb{R}^{3}$

单位四元数表示三维空间中任意一个旋转。 假设某个旋转是绕单位向量$ n = [n_x, n_y, n_z]^T $进行了角度为$\theta$的旋转，那么这个旋转的四元数形式为：

$q = [ \cos \frac { \theta } { 2 } , \boldsymbol{n} _ { x } \sin \frac { \theta } { 2 } , \boldsymbol{n} _ { y } \sin \frac { \theta } { 2 } , \boldsymbol{n} _ { z } \sin \frac { \theta } { 2 } ] ^ { T }$

亦可从单位四元数中计算出对应旋转轴与夹角：

$\left\{\begin{array}{l} \theta=2 \arccos q_{0} \\ {\left[n_{x}, n_{y}, n_{z}\right]^{T}=\left[q_{1}, q_{2}, q_{3}\right]^{T} / \sin \frac{\theta}{2}} \end{array}\right.$

在四元数中， 任意的旋转 都可以由两个互为相反数的四元数表示。

用四元数表示旋转

$\boldsymbol{p} ^ { \prime } = \boldsymbol{q} \boldsymbol{p} \boldsymbol{q} ^ { - 1 }$

四元数到旋转矩阵的转换

$\boldsymbol{R}=\left[\begin{array}{ccc} 1-2 q_{2}^{2}-2 q_{3}^{2} & 2 q_{1} q_{2}+2 q_{0} q_{3} & 2 q_{1} q_{3}-2 q_{0} q_{2} \\ 2 q_{1} q_{2}-2 q_{0} q_{3} & 1-2 q_{1}^{2}-2 q_{3}^{2} & 2 q_{2} q_{3}+2 q_{0} q_{1} \\ 2 q_{1} q_{3}+2 q_{0} q_{2} & 2 q_{2} q_{3}-2 q_{0} q_{1} & 1-2 q_{1}^{2}-2 q_{2}^{2} \end{array}\right]$

$q_{0}=\frac{\sqrt{\operatorname{tr}(R)+1}}{2}, q_{1}=\frac{m_{23}-m_{32}}{4 q_{0}}, q_{2}=\frac{m_{31}-m_{13}}{4 q_{0}}, q_{3}=\frac{m_{12}-m_{21}}{4 q_{0}}$

相似变换

相似变换比欧氏变换多了一个自由度，它允许物体进行均匀的缩放，其矩阵表示为：

$T _ { S } = \left[ \begin{array} { l l } { s R } & { t } \\ { 0 ^ { T } } & { 1 } \end{array} \right]$

仿射变换

与欧氏变换不同的是，仿射变换只要求$ A $是一个可逆矩阵，而不必是正交矩阵。仿射变换也叫正交投影。经过仿射变换之后，立方体就不再是方的了，但是各个面仍然是平行四边形。

$T _ { A } = \left[ \begin{array} { l l } { A } & { t } \\ { 0 ^ { T } } & { 1 } \end{array} \right]$

射影变换

射影变换是最一般的变换，它的矩阵形式为:

$T _ { P } = \left[ \begin{array} { l l } { A } & { t } \\ { a ^ { T } } & { v } \end{array} \right]$

从真实世界到相机照片的变换是一个射影变换。如果相机的焦距为 无穷远，那么这个变换则为仿射变换。