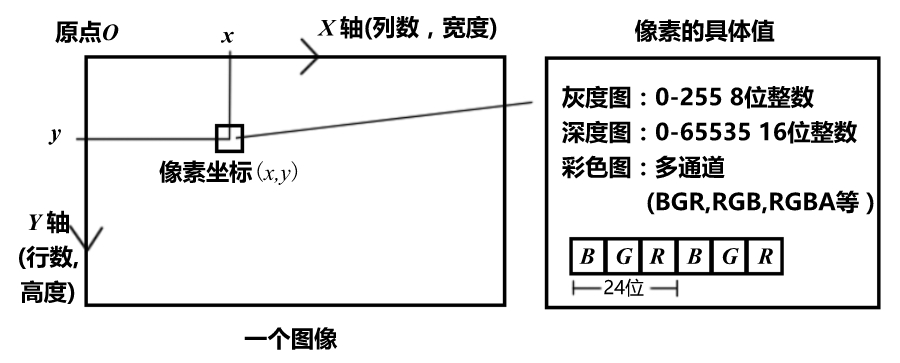
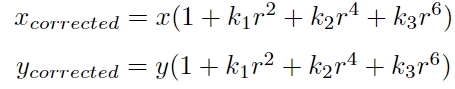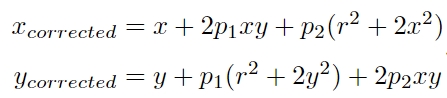相机模型

相机模型

针孔模型和畸变构成了相机的内参数。

针孔相机模型

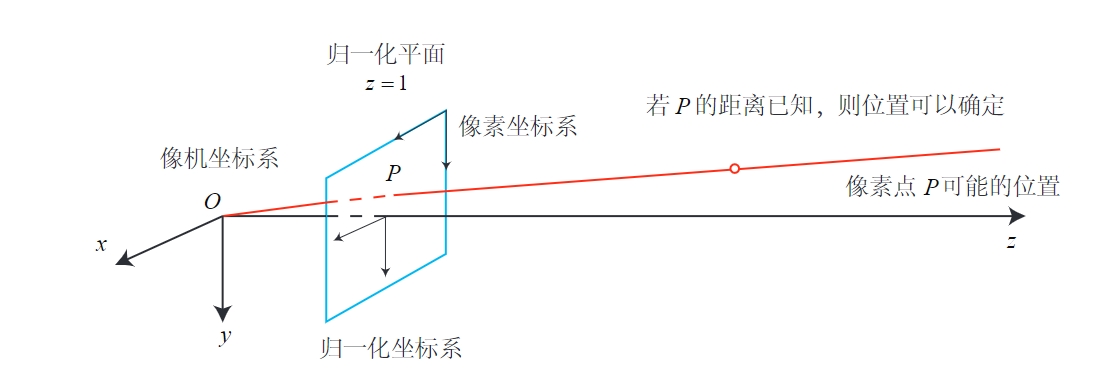
物体与像的数学模型

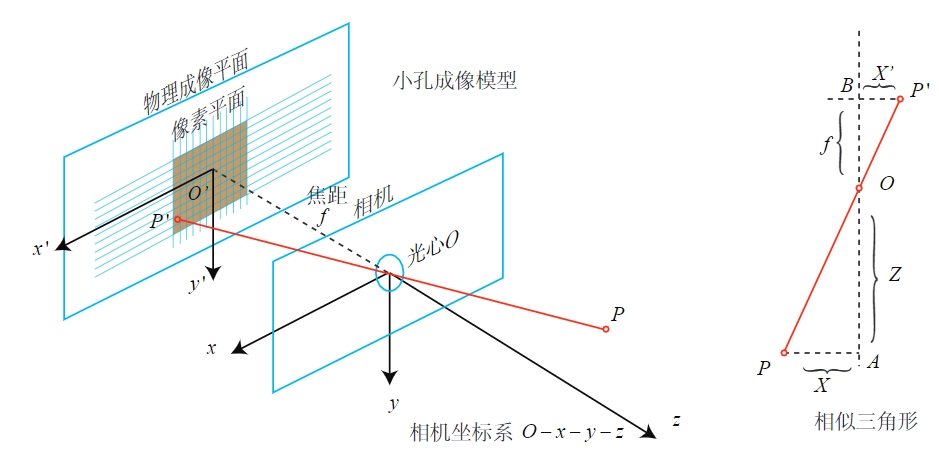
像与像素的数学模型

$\begin{cases} u=\alpha X^{'}+c_x=f_x\frac{X}{Z}+c_x\\ v=\beta Y^{'}+c_y=f_y\frac{Y}{Z}+c_y\\ \end{cases}$

也即：

$Z \left( \begin{array} { l } { u } \\ { v } \\ { 1 } \end{array} \right) = \left( \begin{array} { l } { f _ { x } } & { 0 } & { c _ { x } } \\ { 0 } & { f _ { y } } & { c _ { y } } \\ { 0 } & { 0 } & { 1 } \end{array} \right) \left( \begin{array} { l } { X } \\ { Y } \\ { Z } \end{array} \right) \triangleq K P$

把中间的量组成的矩阵称为相机的内参数矩阵（Camera Intrinsics）$K$。相机的内参在出厂之后是固定的，不会在使用过程中发生变化。

相机的位姿由它的旋转矩阵$ R $和平移向量 t 来描述:

$Z P _ { \mu v } = Z \left[ \begin{array} { l } { u } \\ { v } \\ { 1 } \end{array} \right] = K ( R P _ { w }+ t ) = K T P _ { w }$

相机的位姿$R$,$t$又称为相机的外参数 （Camera Extrinsics）

畸变

透镜的加入对成像过程中光线 的传播会产生新的影响: 一是透镜自身的形状对光线传播的影响，二是在机械组装过程中， 透镜和成像平面不可能完全平行。

径向畸变

由透镜形状引起的畸变称之为径向畸变。

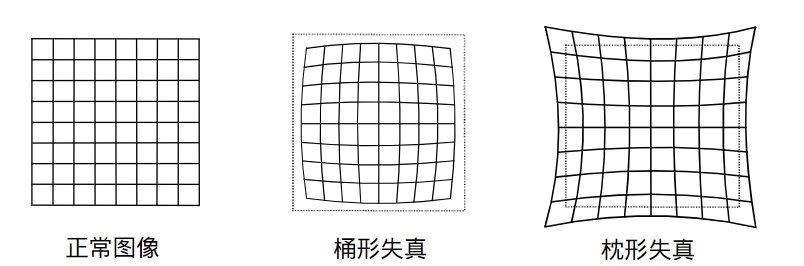
对于径向畸变这类畸变可以用和距中 心距离有关的二次及高次多项式函数进行纠正。

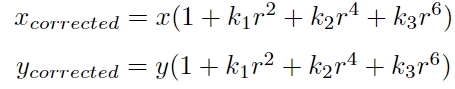
切向畸变

在相机的组装过程中由于不能使得透镜和成像面 严格平行也会引入切向畸变。

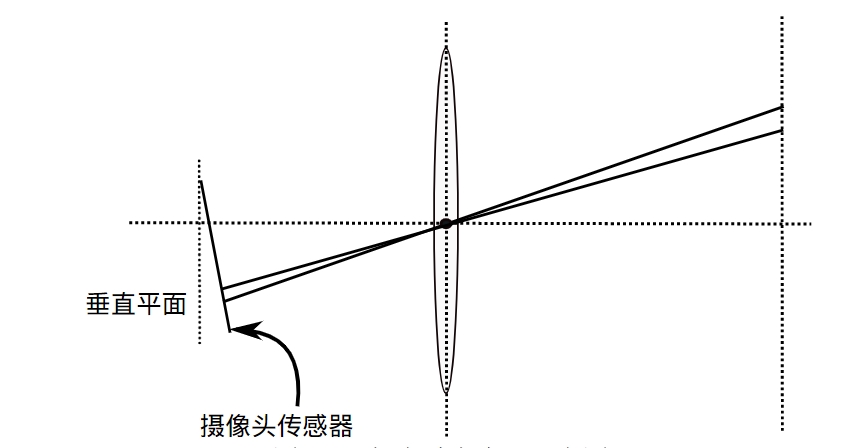
对于切向畸变，可以使用另外的两个参数 p1; p2 来进行纠正:

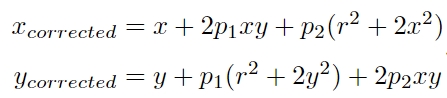
双目相机模型

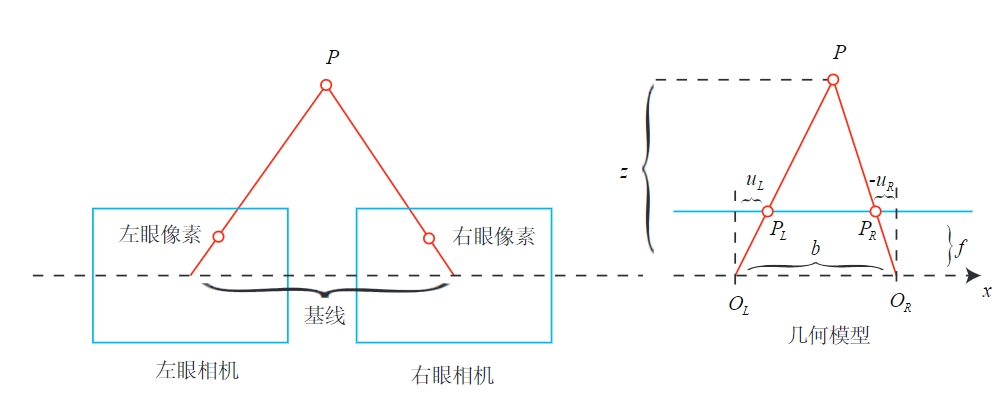
$d = u _ { L } - u _ { R }$

$d$为称为视差

RGB-D 相机模型

• 通过红外结构光 （Structured Light） 来测量像素距离的。 例子有 Kinect 1 代、 Project Tango 1 代、Intel RealSense 等：
  
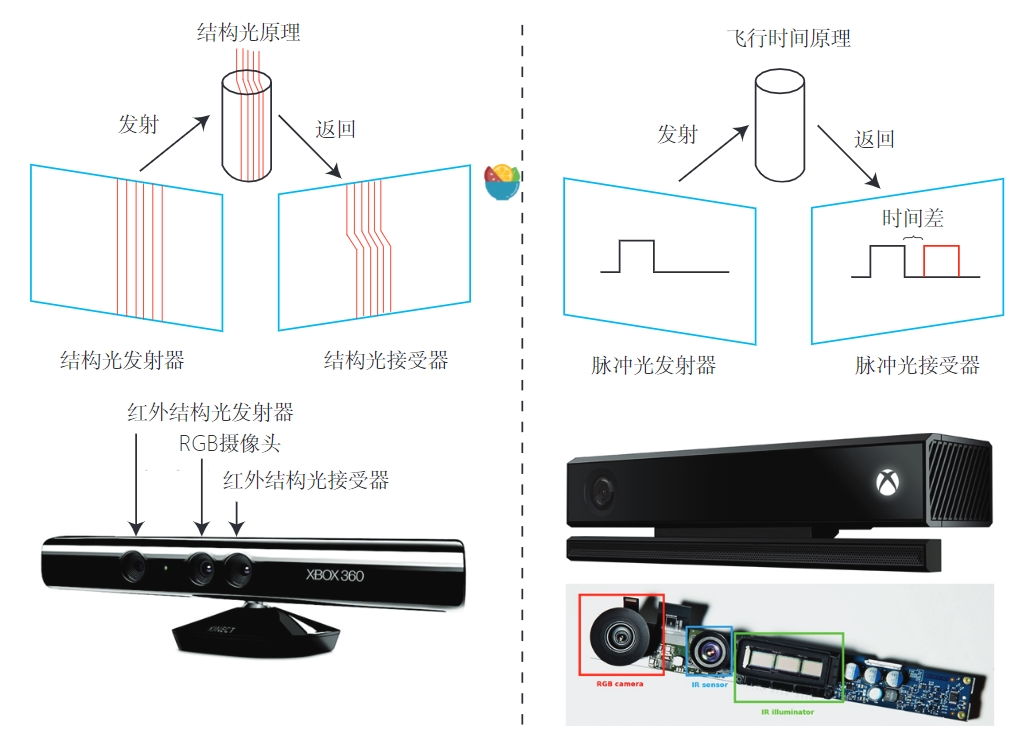
• 通过飞行时间法（Time-of-flight, ToF）原理测量像素距离的。例子有 Kinect 2 代和 一些现有的 ToF 传感器等。