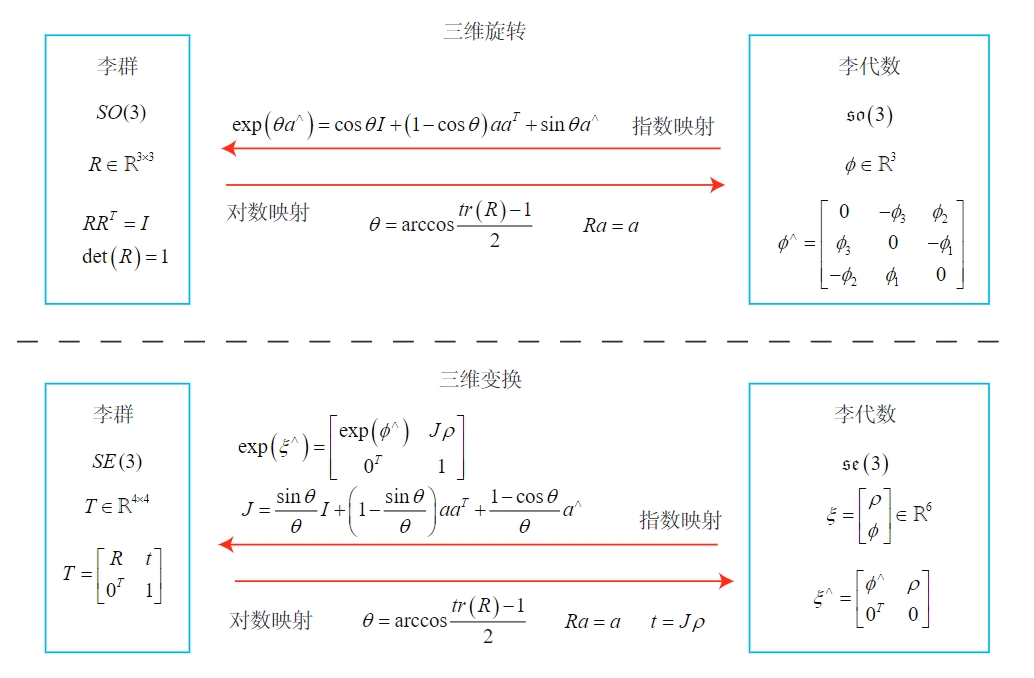
李群与李代数

在 SLAM 中位姿是未知的，而我们需要解决什 么样的相机位姿最符合当前观测数据这样的问题。一种典型的方式是把它构建成一个优化 问题，求解最优的 R;t，使得误差最小化。 通过李群——李代数间的转换关系，旋转矩阵自身是带有约束的（正交且行列式为 1） 。它们作为优化变量时， 会引入额外的约束，使优化变得困难。我们希望把位姿估计变成无约束的优化问题，简化求解方式。

群

三维旋转矩阵构成了特殊正交群 $SO(3)$，而变换矩阵构成了特殊欧氏群$ SE(3)$：

$\begin{gathered} S O(3)=\left\{\boldsymbol{R} \in \mathbb{R}^{3 \times 3} \mid \boldsymbol{R} \boldsymbol{R}^{T}=\boldsymbol{I}, \operatorname{det}(\boldsymbol{R})=1\right\} . \\ S E(3)=\left\{T=\left[\begin{array}{cc} \boldsymbol{R} & t \\ \mathbf{0}^{T} & 1 \end{array}\right] \in \mathbb{R}^{4 \times 4} \mid \boldsymbol{R} \in S O(3), t \in \mathbb{R}^{3}\right\} . \end{gathered}$

李群是指具有连续光滑性质的群。每个李群都有对应的李代数

李代数

$a^{\wedge}=A=\left[\begin{array}{ccc} 0 & -a_{3} & a_{2} \\ a_{3} & 0 & -a_{1} \\ -a_{2} & a_{1} & 0 \end{array}\right], \quad A^{\vee}=a$

$R$是某个相机的旋转，它会随时间连续地变化， 即为时间的函数：$R(t)$:

$R ( t ) R ( t ) ^ { T } = I$

求导得到：

$\dot{R} ( t ) R ( t ) ^ { T } = - ( \dot{R} ( t ) R ( t ) ^ { T } ) ^ { T }$

我们设：$\dot{R} ( t ) R ( t ) ^ { T } = \phi ( t ) ^ { \wedge }$

$\dot{R}(t)=\phi(t)^{\wedge} R(t)=\left[\begin{array}{ccc} 0 & -\phi_{3} & \phi_{2} \\ \phi_{3} & 0 & -\phi_{1} \\ -\phi_{2} & \phi_{1} & 0 \end{array}\right] R(t) .$

我们设$t_0= 0$，并设此时旋转矩阵为$R(0) =I$。按照导数定义，可以把$R(t)$在0附近进行 一阶泰勒展开：

$\left. \begin{array} { l } { R ( t ) \approx R ( t _ { 0 } ) + \dot{R} ( t _ { 0 } ) ( t - t _ { 0 } ) } \\ { = I + \phi ( t _ { 0 } ) ^ { \wedge } (t - t _ {0 }) } \end{array} \right.$

解微分方程得：

$R ( t ) = e x p ( \phi _ { 0 } ^ { \prime } t )$

$s o ( 3 ) = \{ \phi \in \mathbb{R} ^ { 3 } , \varPhi = \phi ^ { \wedge } \in \mathbb{R} ^ { 3 \times 3 } \}$

李括号：

$[ \phi _ { 1 } , \phi _ { 2 } ] = ( \varPhi _ { 1 } \varPhi _ { 2 } - \varPhi_ { 2 } \varPhi_ { 1 } ) ^ { V }$

$\mathfrak{s e}(3)=\left\{\xi=\left[\begin{array}{c} \rho \\ \phi \end{array}\right] \in \mathbb{R}^{6}, \rho \in \mathbb{R}^{3}, \phi \in \mathfrak{s o}(3), \xi^{\wedge}=\left[\begin{array}{cc} \phi^{\wedge} & \rho \\ 0^{T} & 0 \end{array}\right] \in \mathbb{R}^{4 \times 4}\right\}$

李括号为：

$\left[\xi_{1}, \xi_{2}\right]=\left(\xi_{1}^{\wedge} \xi_{2}^{\wedge}-\xi_{2}^{\wedge} \xi_{1}^{\wedge}\right)^{\vee}$

根据性质：

$\begin{cases} \left. a^{\land}a^{\land}=aa^T-\boldsymbol{I} \right.\\ a^{\land}a^{\land}a^{\land}=-a^{\land}\\ \end{cases}$

得到：

$\begin{aligned} \exp \left(\phi^{\wedge}\right) &=\exp \left(\theta \boldsymbol{a}^{\wedge}\right)=\sum_{n=0}^{\infty} \frac{1}{n !}\left(\theta \boldsymbol{a}^{\wedge}\right)^{n} \\ &=\boldsymbol{I}+\theta \boldsymbol{a}^{\wedge}+\frac{1}{2 !} \theta^{2} \boldsymbol{a}^{\wedge} \boldsymbol{a}^{\wedge}+\frac{1}{3 !} \theta^{3} \boldsymbol{a}^{\wedge} \boldsymbol{a}^{\wedge} \boldsymbol{a}^{\wedge}+\frac{1}{4 !} \theta^{4}\left(\boldsymbol{a}^{\wedge}\right)^{4}+\ldots \\ &=\boldsymbol{a} \boldsymbol{a}^{T}-\boldsymbol{a}^{\wedge} \boldsymbol{a}^{\wedge}+\theta \boldsymbol{a}^{\wedge}+\frac{1}{2 !} \theta^{2} \boldsymbol{a}^{\wedge} \boldsymbol{a}^{\wedge}-\frac{1}{3 !} \theta^{3} \boldsymbol{a}^{\wedge}-\frac{1}{4 !} \theta^{4}\left(\boldsymbol{a}^{\wedge}\right)^{2}+\ldots \\ &=\boldsymbol{a} \boldsymbol{a}^{T}+\left(\theta-\frac{1}{3 !} \theta^{3}+\frac{1}{5 !} \theta^{5}-\ldots\right) \boldsymbol{a}^{\wedge}-\left(1-\frac{1}{2 !} \theta^{2}+\frac{1}{4 !} \theta^{4}-\ldots\right) \boldsymbol{a}^{\wedge} \boldsymbol{a}^{\wedge} \\ &=\boldsymbol{a}^{\wedge} \boldsymbol{a}^{\wedge}+\boldsymbol{I}+\sin \theta \boldsymbol{a}^{\wedge}-\cos \theta \boldsymbol{a}^{\wedge} \boldsymbol{a}^{\wedge} \\ &=(1-\cos \theta) \boldsymbol{a}^{\wedge} \boldsymbol{a}^{\wedge}+\boldsymbol{I}+\sin \theta \boldsymbol{a}^{\wedge} \\ &=\cos \theta \boldsymbol{I}+(1-\cos \theta) \boldsymbol{a} \boldsymbol{a}^{T}+\sin \theta \boldsymbol{a}^{\wedge} . \end{aligned}$

$\mathfrak{s} \mathfrak{o}(3)$ 实际上就是由所谓的旋转向量组成的空间，而指数映射即罗德里格斯公式。
通过它们，我们把$\mathfrak{s} \mathfrak{o}(3)$ 中任意一个向量对应到了一个位于$ SO(3) $中的**旋转矩阵**。反之，如果定义对数映射， 我们也能把$ SO(3) $中的元素对应到$\mathfrak{s} \mathfrak{o}(3)$ 中：

$\phi=\ln (\boldsymbol{R})^{\vee}=\left(\sum_{n=0}^{\infty} \frac{(-1)^{n}}{n+1}(\boldsymbol{R}-\boldsymbol{I})^{n+1}\right)^{\vee}$

旋转矩阵的导数可以由旋转向量指定，指导着 如何在旋转矩阵中进行微积分运算。

$\mathfrak{s} \mathfrak{e}(3)$ 上的指数映射形式如下：

$\begin{aligned} \exp \left(\boldsymbol{\xi}^{\wedge}\right) &=\left[\begin{array}{ccc} \sum_{n=0}^{\infty} \frac{1}{n !}\left(\boldsymbol{\phi}^{\wedge}\right)^{n} & \sum_{n=0}^{\infty} \frac{1}{(n+1) !}\left(\boldsymbol{\phi}^{\wedge}\right)^{n} \boldsymbol{\rho} \\ & \mathbf{0}^{T} \end{array}\right] \\ & \triangleq\left[\begin{array}{cc} \boldsymbol{R} & \boldsymbol{J} \boldsymbol{\rho} \\ \mathbf{0}^{T} & 1 \end{array}\right]=\boldsymbol{T} . \end{aligned}$

我们设$\phi = \theta \boldsymbol{a}$

$\boldsymbol{J}=\frac{\sin \theta}{\theta} \boldsymbol{I}+\left(1-\frac{\sin \theta}{\theta}\right) \boldsymbol{a} \boldsymbol{a}^{T}+\frac{1-\cos \theta}{\theta} \boldsymbol{a}^{\wedge}$

李代数求导与扰动模型

BCH公式与近似形式

两个李代数指数映射乘积的完整形式，由 Baker-Campbell-Hausdorff 公式（BCH公式）给出。由于它完整的形式较复杂，我们给出它展开式的前几项：

$\ln ( \exp ( A ) \exp ( B ) ) = A + B + \frac { 1 } { 2 } [ A , B ] + \frac { 1 } { 12 } [ A , [ A , B ] ] - \frac { 1 } { 12 } [ B , [ A , B ] ] + \cdots$

当 $\phi_1$ 或$\phi_2$为小量时，小量二次以上的项都可以被忽略掉。此时，BCH 拥有线性近似表达：

$\ln \left(\exp \left(\phi_{1}^{\wedge}\right) \exp \left(\phi_{2}^{\wedge}\right)\right)^{\vee} \approx\left\{\begin{array}{cc} \boldsymbol{J}_{l}\left(\phi_{2}\right)^{-1} \phi_{1}+\phi_{2} & \text { if } \phi_{1} \text { is small } \\ \boldsymbol{J}_{r}\left(\phi_{1}\right)^{-1} \phi_{2}+\phi_{1} & \text { if } \phi_{2} \text { is small } \end{array}\right.$

$SO(3)$李代数上的求导

位姿估计相当于是寻找一个最优的$ T$，使得整体误差最小化：

$\min _ { T } J ( T ) = \sum _ { i = 1 } ^ { N } | | z _ { i } - T p _ { i } | |_2 ^ { 2 }$

我们经常会构建与位姿有关的函数，然后讨论该函数关于位姿的导数，以调整当前的估计值。

李代数求导

$\frac { \partial ( \boldsymbol{R} p ) } { \partial \phi } = ( - R p ) ^ { \wedge } J _ { t }$

扰动模型（左乘）

$\begin{aligned} \frac{\partial(\boldsymbol{R} p)}{\partial \varphi} &=\lim _{\varphi \rightarrow 0} \frac{\exp \left(\varphi^{\wedge}\right) \exp \left(\phi^{\wedge}\right) p-\exp \left(\phi^{\wedge}\right) p}{\varphi} \\ & \approx \lim _{\varphi \rightarrow 0} \frac{\left(1+\varphi^{\wedge}\right) \exp \left(\phi^{\wedge}\right) p-\exp \left(\phi^{\wedge}\right) p}{\varphi} \\ &=\lim _{\varphi \rightarrow 0} \frac{\varphi^{\wedge} \boldsymbol{R} p}{\varphi}=\lim _{\varphi \rightarrow 0} \frac{-(\boldsymbol{R} p)^{\wedge} \varphi}{\varphi}=-(\boldsymbol{R} p)^{\wedge} \end{aligned}$

$SE(3)$上的李代数求导

$\begin{aligned} \frac{\partial(\boldsymbol{T} \boldsymbol{p})}{\partial \delta \boldsymbol{\xi}} &=\lim _{\delta \boldsymbol{\xi} \rightarrow 0} \frac{\exp \left(\delta \boldsymbol{\xi}^{\wedge}\right) \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{p}-\exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{p}}{\delta \boldsymbol{\xi}} \\ & \approx \lim _{\delta \boldsymbol{\xi} \rightarrow 0} \frac{\left(\boldsymbol{I}+\delta \boldsymbol{\xi}^{\wedge}\right) \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{p}-\exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{p}}{\delta \boldsymbol{\xi}} \\ &=\lim _{\delta \boldsymbol{\xi} \rightarrow 0} \frac{\delta \boldsymbol{\xi}^{\wedge} \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{p}}{\delta \boldsymbol{\xi}} \\ &=\lim _{\delta \boldsymbol{\xi} \rightarrow 0} \frac{\left[\begin{array}{cc} \delta \boldsymbol{\phi}^{\wedge} & \delta \boldsymbol{\rho} \\ \mathbf{0}^{T} & 0 \end{array}\right]\left[\begin{array}{c} \boldsymbol{R} \boldsymbol{p}+\boldsymbol{t} \\ 1 \end{array}\right]}{\delta \boldsymbol{\xi}} \\ &=\lim _{\delta \boldsymbol{\xi} \rightarrow 0} \frac{\left[\begin{array}{cc} \delta \boldsymbol{\phi}^{\wedge}(\boldsymbol{R} \boldsymbol{p}+\boldsymbol{t})+\delta \boldsymbol{\rho} \\ 0 \end{array}\right]}{\delta \boldsymbol{\xi}}=\left[\begin{array}{cc} \boldsymbol{I} & -(\boldsymbol{R} \boldsymbol{p}+\boldsymbol{t})^{\wedge} \\ 0^{T} & \mathbf{0}^{T} \end{array}\right] \triangleq(\boldsymbol{T} \boldsymbol{p})^{\odot} . \end{aligned}$