数字基带传输系统

数字基带信号及其频谱特性

设计归零信号的意义：由于其相邻脉冲之间存在零电位的间隔，使得接收端很容易识别出每个码元的起止时刻。

设置双极性的意义：提高抗干扰能力。

差分波形传输信息可以消除设备初始状态的影响。

基带信号的频谱特性

• 数字基带信号是一个随机脉冲序列，没有确定的频谱函数，所以只能用功率谱来描述它的频谱特性。
  下面推导数字基带信号的功率谱密度：
  设数字基带信号为$s(t)$

$s\left( t \right) =\sum_{n=-\infty}^{\infty}{s_n\left( t \right)}$

其中：

$s_n\left( t \right) =\begin{cases} g_1\left( t-nT_B \right) \,\, \text{以概率}P\text{出现}\\ g_2\left( t-nT_B \right) \,\, \text{以概率}\left( 1-P \right) \text{出现}\\ \end{cases}$

将$s(t)$分为稳态波$v(t)$和交态波$u(t)$

$v(t)=\sum_{n=-\infty}^{\infty}{\left[ Pg_1\left( t-nT_{\mathrm{B}} \right) +(1-P)g_2\left( t-nT_{\mathrm{B}} \right) \right]}=\sum_{n=-\infty}^{\infty}{v_n}(t)$

$P_{v}(f)$的计算

可知$v(t)$以$T_B$为周期的周期函数，而交变波为：

$u(t)=s(t)-v(t)$

同时可以写为：

\begin{equation} \begin{split} u_n\left( t \right)& =s_n\left( t \right) -v_n\left( t \right) \\ &=a_n\left[ g_1\left( t-nT_B \right) -g_2\left( t-nT_B \right) \right] \end{split} \nonumber \end{equation}

其中

$a_n=\begin{cases} 1-P\,\, \text{以概率}P\\ -P\,\, \text{以概率}\left( 1-P \right)\\ \end{cases}$

$v\left( t \right) =\sum_{m=-\infty}^{\infty}{C_me^{j2\pi mf_Bt}}\,\, \text{其中} \left( f_B=\frac{1}{T_B} \right)$

其中傅里叶系数$C_m$

$C_m=f_B\left[ PG_1\left( mf_B+\left( 1-P \right) G_2\left( mf_B \right) \right) \right]$

由此可知功率谱密度为：

$P_{v}(f)=\sum_{m=-\infty}^{\infty}\left|f_{\mathrm{B}}\left[P G_{1}\left(m f_{\mathrm{B}}\right)+(1-P) G_{2}\left(m f_{\mathrm{B}}\right)\right]\right|^{2} \delta\left(f-m f_{\mathrm{B}}\right)$

上式表明稳态波$v(T)$的功率谱$P_{v}(f)$是冲击强度取决于$|C_m|^2$的离散线谱。

$P_{u}(f)$的计算

通过式：

$\begin{cases} P_u\left( f \right) =\lim_{T\rightarrow \infty} \frac{\mathbb{E} \left[ |U_T\left( f \right) |^2 \right]}{T}\\ T=\left( 2N+1 \right) T_B\\ U_T\left( f \right) =\mathscr{F} \left[ u_T\left( t \right) \right]\\ u_T\left( t \right) =\sum_{n=-N}^N{a_n}\left[ g_1\left( t-nT_{\mathrm{B}} \right) -g_2\left( t-nT_{\mathrm{B}} \right) \right]\\ \end{cases}$

求得：

$P_u\left( f \right) =f_BP\left( 1-P \right) |G_1\left( f \right) -G_2\left( f \right) |^2$

又由$s(t)=v(t)+u(t)$可得：

$\begin{aligned} P_{\mathrm{s}}(f)=& P_{u}(f)+P_{v}(f)=f_{\mathrm{B}} P(1-P)\left|G_{1}(f)-G_{2}(f)\right|^{2}+\\ & \sum_{m=-\infty}^{\infty}\left|f_{\mathrm{B}}\left[P G_{1}\left(m f_{\mathrm{B}}\right)+(1-P) G_{2}\left(m f_{\mathrm{B}}\right)\right]\right|^{2} \delta\left(f-m f_{\mathrm{B}}\right) \end{aligned}$

写成单边：

$\begin{aligned} P_{\mathrm{s}}(f)=& 2 f_{\mathrm{B}} P(1-P)\left|G_{1}(f)-G_{2}(f)\right|^{2}+f_{\mathrm{B}}^{2}\left|P G_{1}(0)+(1-P) G_{2}(0)\right|^{2} \delta(f)+\\ & 2 f_{\mathrm{B}}^{2} \sum_{m=1}^{\infty}\left|P G_{1}\left(m f_{\mathrm{B}}\right)+(1-P) G_{2}\left(m f_{\mathrm{B}}\right)\right|^{2} \delta\left(f-m f_{\mathrm{B}}\right) \quad f \geqslant 0 \end{aligned}$

由此可以得出结论：

• $P_{\mathrm{s}}(f)$可能包含离散谱和连续谱
• 连续谱一定存在，离散谱不一定存在
• 对于双极性信号，-1和+1波形出现概率相等时没有离散谱

常用码型

AMI码

• 优点：没有直流分量
• 缺点：提取定时信号困难

HDB3

无码间干扰

码间串扰产生的原因是由于系统总传输特性的不理想，使前面码元波形的拖尾蔓延到当前码元的抽样时刻上，从而对当前码元的判决造成干扰；

无码间干扰条件

• 时域：

$h\left( kT_s \right) =\begin{cases} C\,\, ,k=0\\ 0 , k\ne 0\\ \end{cases}$

• 频域：

$H_{eq}\left( w \right) =\sum_i{H\left( w+i\frac{2\pi}{T_s} \right) =C, |w|\le \frac{\pi}{T_s}}$

部分响应系统

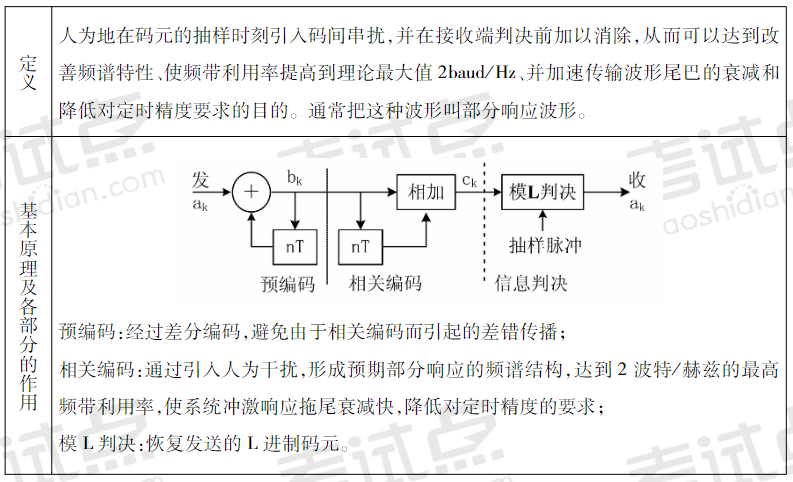
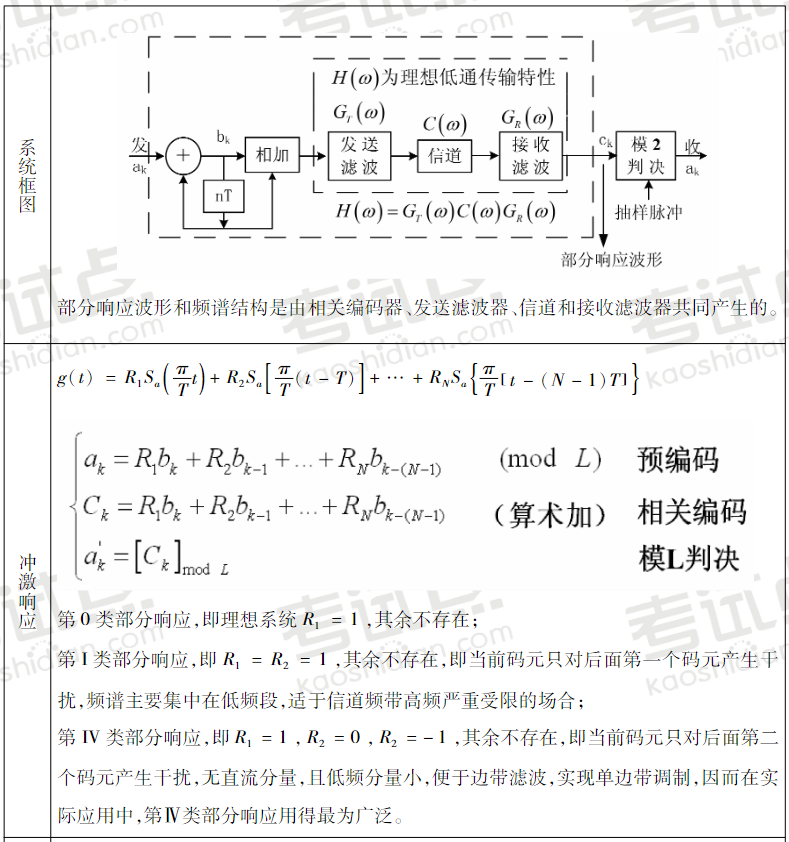
当输入数据为Ｌ进制时，第Ｉ和第ＩＶ相关编码电平数为２Ｌ－１，因此，抗噪声性能变差，但是以上两类的抽样值电平数比其它类别的少，这使得其判决时噪声容限较大，误码率较低。

眼图及其模型

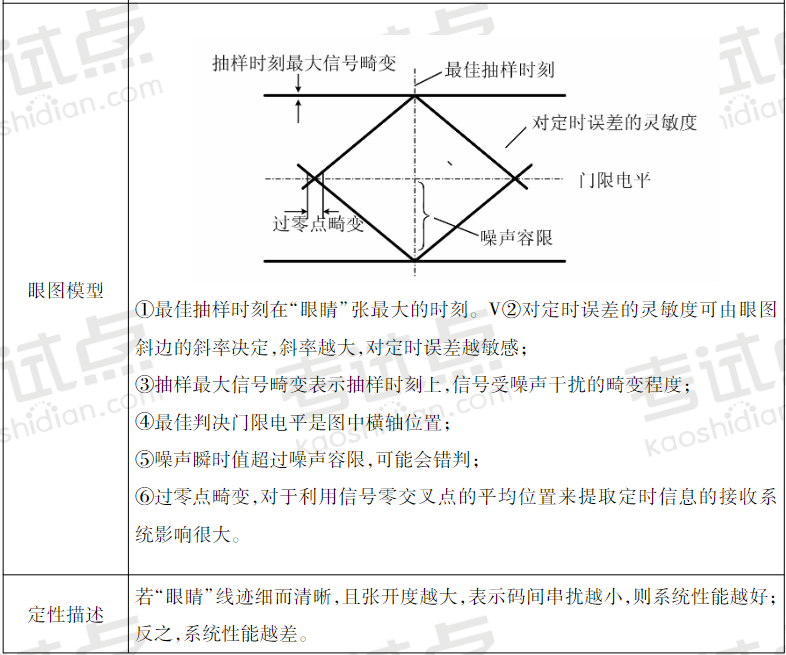
均衡技术

在基带系统中插入一种可调（或不可调）滤波器可以校正或补偿系统特性，减小码间串扰的影响，这种起补偿作用的滤波器成为均衡器。

• 频域均衡：从校正系统的频域出发，使包括均衡器在内的基带系统的总特性满足无失真传输条件
• 时域均衡：是利用均衡器产生的时间波形取直接矫正已畸变的波形，使包括均衡器在内的整个系统的冲击响应满足无码间串扰条件。