即时到位与建图

传感器

一类传感器是携带于机器人本体上的， 例如机器人的轮式编码器、 相机、 激光等等。 另 一类是安装于环境中的，例如前面讲的导轨、二维码标志等等。安装于环境中的传感设备， 通常能够直接测量到机器人的位置信息，简单有效地解决定位问题。然而，由于它们必须 在环境中设置，在一定程度上限制了机器人的使用范围。

普通的摄像头能以每秒钟30张图片的速度采集图像，高速相机则更快一些。按照相机的工作方式，我们把相机分为单目（Monocular） 、双目（Stereo）和深度相机（RGB-D）三个大类，

视觉slam框架

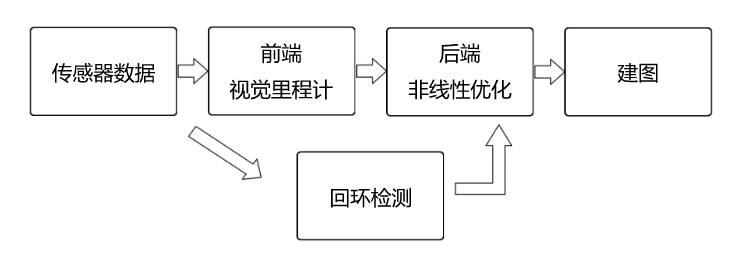
整个视觉 SLAM 流程分为以下几步：

• 1. 传感器信息读取。在视觉 SLAM 中主要为相机图像信息的读取和预处理。如果在机器人中，还可能有码盘、惯性传感器等信息的读取和同步。
• 2. 视觉里程计 (Visual Odometry, VO)。 视觉里程计任务是估算相邻图像间相机的运动， 以及局部地图的样子。VO 又称为前端（Front End） 。
• 3. 后端优化（Optimization） 。后端接受不同时刻视觉里程计测量的相机位姿，以及回环检测的信息，对它们进行优化，得到全局一致的轨迹和地图。由于接在 VO 之后， 又称为后端（Back End） 。
• 4. 回环检测（Loop Closing） 。回环检测判断机器人是否曾经到达过先前的位置。如果检测到回环，它会把信息提供给后端进行处理。
• 5. 建图（Mapping） 。它根据估计的轨迹，建立与任务要求对应的地图。

如果把工作环境限定在静态、刚体，光照变化不明显、没有人为干 扰的场景，那么，这个 SLAM 系统是相当成熟的了。

叫它为“里程计”是因为它和实际的里程计一样，只计算相邻时刻的运动，而和再往前的 过去的信息没有关联。然 而， 仅通过视觉里程计来估计轨迹， 将不可避免地出现累计漂移（Accumulating Drift） 。 这 是由于视觉里程计（在最简单的情况下）只估计两个图像间运动造成的。

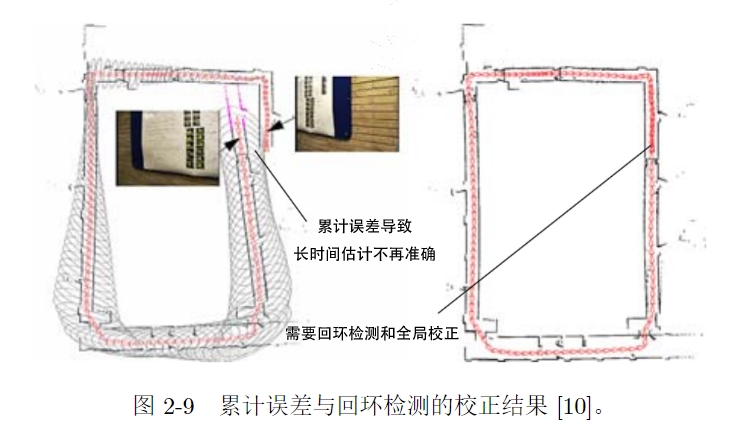
这也就是所谓的漂移（Drift） 。 它将导致我们无法建立一致的地图。 你会发现原本直的 走廊变成了斜的，为了解决漂移问题，我们还需要两种技术：后端优化 ̈ 和回环检测。回环检测负责把“机器 人回到原始位置”的事情检测出来，而后端优化则根据该信息，校正整个轨迹的形状。

后端优化主要指处理 SLAM 过程中噪声的问题，除了解决“如何从图 像估计出相机运动”之外，我们还要关心这个估计带有多大的噪声，这些噪声是如何从上 一时刻传递到下一时刻的、而我们又对当前的估计有多大的自信。后端优化要考虑的问题， 就是如何从这些带有噪声的数据中，估计整个系统的状态，以及这个状态估计的不确定性 有多大——这称为最大后验概率估计（Maximum-a-Posteriori，MAP。。在 SLAM 框架中，前端给后端提供 待优化的数据，以及这些数据的初始值。而后端负责整体的优化过程，它往往面对的只有 数据，不必关心这些数据到底来自什么传感器。在视觉 SLAM 中，前端和计算机视觉研 究领域更为相关，比如图像的特征提取与匹配等，后端则主要是滤波与非线性优化算法。

SLAM 问题的本质： 对运动 主体自身和周围环境空间不确定性的估计。

回环检测，又称闭环检测（Loop Closure Detection） ，主要解决位置估计随时间漂移 的问题。地图存在的主要意义，是为了让机器人知晓自己到达过的地方。为了实现回环检测，我们需要让机 器人具有识别曾到达过的场景的能力。

建图（Mapping）是指构建地图的过程。地图是对环境的描述，但这个描述并不是固 定的，需要视 SLAM 的应用而定。大体上讲，它们可以分为度量地图与拓扑地图两种。

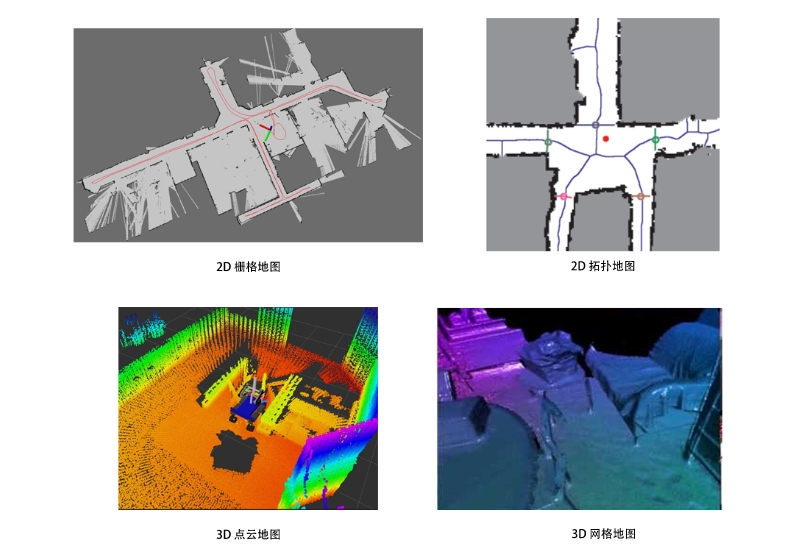
度量地图

通常我们用稀疏（Sparse）与稠密 （Dense） 对它们进行分类。 稀疏地图进行了一定程度的抽象， 并不需要表达所有的物体。 例 如，我们选择一部分具有代表意义的东西，称之为路标（Landmark） ，那么一张稀疏地图 就是由路标组成的地图，而不是路标的部分就可以忽略掉。相对的，稠密地图着重于建模 所有看到的东西。对于定位来说，稀疏路标地图就足够了。

拓扑地图

相比于度量地图的精确性，拓扑地图则更强调地图元素之间的关系。拓扑地图是一个 图（Graph） ，由节点和边组成，只考虑节点间的连通性，例如 A，B 点是连通的，而不考 虑如何从 A 点到达 B 点的过程。它放松了地图对精确位置的需要，去掉地图的细节问题， 是一种更为紧凑的表达方式。

数学建模

运动方程

$\boldsymbol{x}_{k}=f\left(\boldsymbol{x}_{k-1}, \boldsymbol{u}_{k}, \boldsymbol{w}_{k}\right)$

$\boldsymbol{u}_{k}$为运动传感器的读数（有时也叫输入），$\boldsymbol{w}_{k}$为噪声。$\boldsymbol{x}_k$为$k$时刻机器人的位置。

观测方程

$\boldsymbol{z}_{k,j} = h(\boldsymbol{y}_j, \boldsymbol{x}_k, \boldsymbol{v}_{k,j})$

表示机器人在位置$\boldsymbol{x}_k$时刻看到某个路标点$\boldsymbol{y}_j$，产生一个观测数据$\boldsymbol{z}_{k,j}$，$\boldsymbol{v}_{k,j}$为观测的噪声。

SLAM总结为两个基本方程：

$\left\{\begin{array}{l} \boldsymbol{x}_{k}=f\left(\boldsymbol{x}_{k-1}, \boldsymbol{u}_{k}, \boldsymbol{w}_{k}\right) \\ \boldsymbol{z}_{k, j}=h\left(\boldsymbol{y}_{j}, \boldsymbol{x}_{k}, \boldsymbol{v}_{k, j}\right) \end{array}\right.$

当我们知道运动测量的读数$\boldsymbol{u}$， 以及传感器的读数$\boldsymbol{z}$ 时，如何求解定位问题（估计 $\boldsymbol{x}$）和建图问题（估计 $\boldsymbol{y}$）？这时，我们把 SLAM 问题建模成了一个状态估计问题：如何通过带有噪声的测量数据，估计内部的、隐藏着的 状态变量？

线性高斯系统（Linear Gaussian, LG 系统

运动和观测方程为线性，噪声服从高斯分布，它的无偏的最优估计可以由卡尔曼滤波器（Kalman Filter, KF）给出。

在复杂的非线性非高斯系统 （Non-Linear Non-Gaussian， NLNG 系统） 中， 我们会使用以扩展卡尔曼滤波器 （Extended Kalman Filter, EKF）和非线性优化两大类方法去求解它。

为了克服 EKF 的缺点（例如线性化误差和噪声高斯分布假设），人们开 始使用粒子滤波器（Particle Filter）等其他滤波器，乃至使用非线性优化的方法。时至今日，主流视觉 SLAM 使用以图优化（Graph Optimization）为代表的优化技术进行状态估计。只要计算资源允许，我们通常都偏 向于使用优化方法。